filmov
tv
A Differential Equation in Terms of y
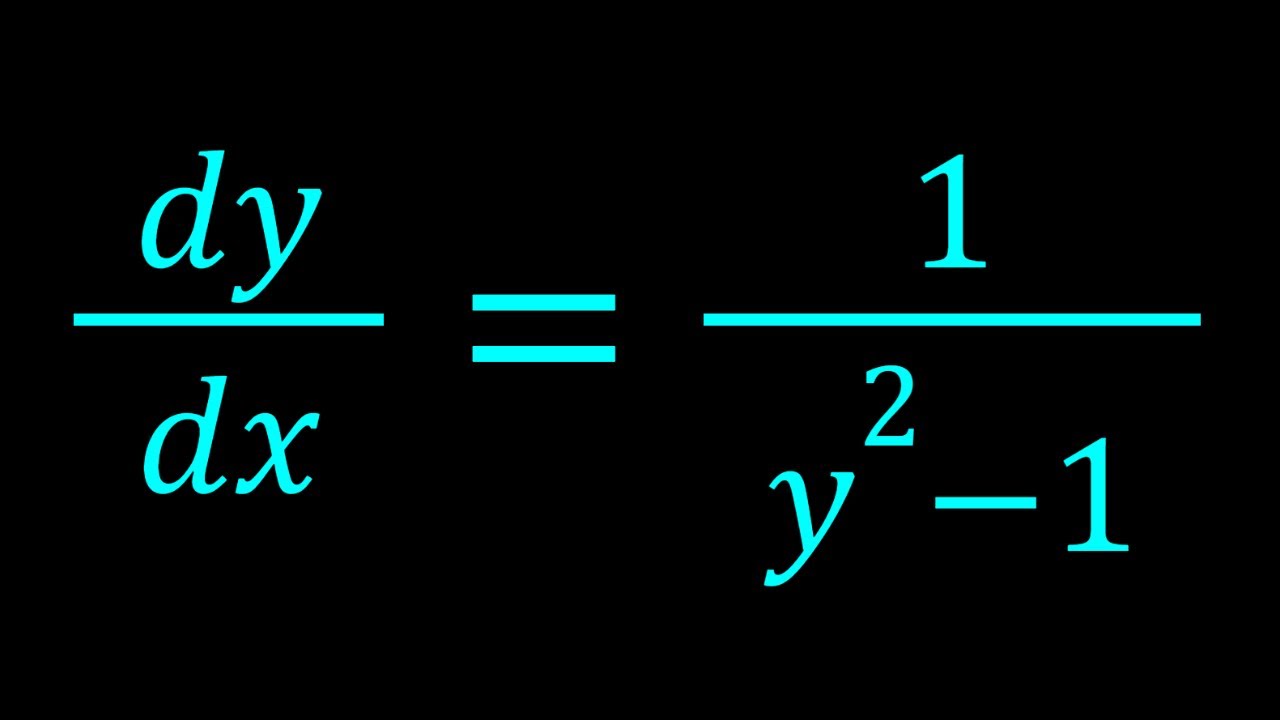
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#CalculusProblems #DifferentialEquations #Calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
#exponentials #exponentialequations #exponential #exponents #challengingmathproblems #maths #math
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#CalculusProblems #DifferentialEquations #Calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
#exponentials #exponentialequations #exponential #exponents #challengingmathproblems #maths #math
the differential equations terms you need to know.
Differential equations, a tourist's guide | DE1
4 Types of ODE's: How to Identify and Solve Them
Differential equation introduction | First order differential equations | Khan Academy
Introduction to Differential Equation Terminology
This is why you're learning differential equations
What are differential equations?
Differential Equations - 5 - Classification
Differential Equation Solution: How to solve Differential Equations by Variable Separation method.
First Order Linear Differential Equations
How to solve differential equations
Separable First Order Differential Equations - Basic Introduction
Differential Equation in terms of Dependent Variable (1 of 2: Partial Fractions)
Differential Equations: Basic Definitions and Terminology (Section 1.1) | Math with Professor V
A Differential Equation in Terms of y
Linear Differential Equation dy/dx + y = e^(6x) ||Transient Terms || Largest Interval Defined
How to Solve Constant Coefficient Homogeneous Differential Equations
Differential Equations Introduction | Differential Calculus Basics #differentialequation
Differential Equations - Introduction, Order and Degree, Solutions to DE
Solving Differential Equations with Power Series
Standard Differential Equation for LTI Systems
Solving an Exact Differential Equation
Difference between linear and nonlinear Differential Equation|Linear verses nonlinear DE
INTRODUCTION TO DIFFERENTIAL EQUATION | Ordinary/Partial | Linear | Order | Degree | TAGALOG-ENGLISH
Комментарии
 0:01:00
0:01:00
 0:27:16
0:27:16
 0:06:57
0:06:57
 0:07:49
0:07:49
 0:07:08
0:07:08
 0:18:36
0:18:36
 0:03:41
0:03:41
 0:07:25
0:07:25
 0:00:00
0:00:00
 0:22:28
0:22:28
 0:00:46
0:00:46
 0:10:42
0:10:42
 0:10:44
0:10:44
 0:23:56
0:23:56
 0:09:03
0:09:03
 0:08:33
0:08:33
 0:06:41
0:06:41
 0:18:50
0:18:50
 0:34:59
0:34:59
 0:18:29
0:18:29
 0:14:01
0:14:01
 0:02:46
0:02:46
 0:03:29
0:03:29
 0:20:40
0:20:40