filmov
tv
Solving A Nonstandard Equation in Two Ways

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#exponentialequations #algebra #logarithms
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#exponentialequations #algebra #logarithms
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving A Nonstandard Equation in Two Ways
Solving a Non-Standard Equation For Reals
Let's Solve A Nonstandard Equation
Solving an Equation in Non-standard Ways
Solving A Non-Standard Equation
Solving an equation in non-standard ways
Solving A Rational Equation in A Non-Standard Way
Let's Solve A Nonstandard Equation
Can We Solve A Nonstandard Equation? 😮
A Non-Standard Equation With One Solution
Solving a very radical equation using a non-standard method. An algebraic challenge...
A Non-Standard Equation with One Solution (k is positive)
How To Solve A Non Standard Equation
Can We Solve A Nonstandard Equation?
Solving a Non-Standard Equation, 2^{x^2}=1-x^8
Solving a non-standard equation
Solving A Nonstandard Equation | Problem 150
Can You Solve A Nonstandard Equation?
Let's Solve A Nonstandard Equation | Problem 211
Solving 2^x=x+(1/x), a Non-Standard Equation
Can You Solve a Nonstandard Equation?
A Non-standard Exponential Equation
BEST Method to Solve this Non-Standard OLYMPIAD Exponential Equation | X=?
Solving A Non-Standard Equation | A Special Function
Комментарии
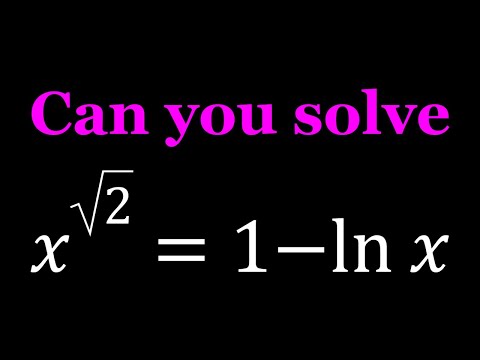 0:08:57
0:08:57
 0:04:34
0:04:34
 0:08:51
0:08:51
 0:16:41
0:16:41
 0:09:05
0:09:05
 0:16:41
0:16:41
 0:10:55
0:10:55
 0:08:42
0:08:42
 0:10:24
0:10:24
 0:09:22
0:09:22
 0:06:54
0:06:54
 0:08:42
0:08:42
 0:04:34
0:04:34
 0:07:24
0:07:24
 0:07:27
0:07:27
 0:08:15
0:08:15
 0:08:57
0:08:57
 0:09:50
0:09:50
 0:08:33
0:08:33
 0:10:18
0:10:18
 0:04:23
0:04:23
 0:04:35
0:04:35
 0:10:03
0:10:03
 0:10:41
0:10:41