filmov
tv
Calculus 2: Applications - Calculating Work (13 of 16) Cal. Work Ex. 12: 1/2-Spherical Tank: 1

Показать описание
In this video I will calculate W=? of pumping all the water out of a semi-spherical tank, part 1.
Next video in the series can be seen at:
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial
Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration
Calculus 2: Applications - Calculating Work (3 of 16) Work Ex 2: Springs NOTE: W=(1/2)kx^2
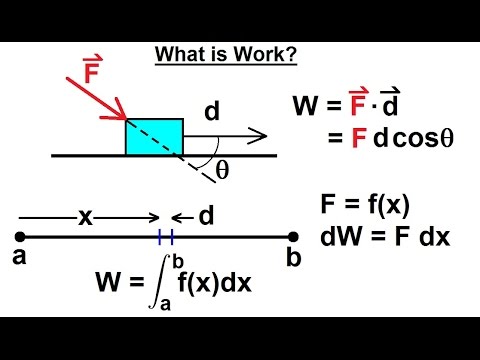
Calculus 2: Applications - Calculating Work (1 of 16) What is Work?
Calculus 2: Applications - Calculating Work (4 of 16) Calculating Work Example 3: Chain
Work Problems - Calculus
Calculus 2: Applications - Calculating Work (8 of 16) Calculating Work Example 7: Elevator
Work Problems | Calculus 2 Lesson 8 - JK Math
Applications of Integrals | One Shot | 12th class #k2institute #integral
Calculus 2: Applications - Calculating Work (15 of 16) Calculating Work Ex. 14: Work Done by a Gas
Calculus 2: Applications - Calculating Work (5 of 16) Calculating Work Example 4: Cone
Calculate Work to Pump Liquid Out of Tanks - Calculus 2
Calculus 2: Applications - Calculating Work (2 of 16) Calculating Work Example 1
Calculus 2: Applications - Calculating Work (14 of 16) Cal. Work Ex. 12: 1/2-Spherical Tank: 2
Calculus 2: Applications - Calculating Work (16 of 16) Calculating Work Ex. 15: Pushing Charges
Calculus 2: Applications - Calculating Work (10 of 16) Calculating Work Example 9: Trough (Part 2)
Differential Equation Mixing Problem, calculus 2 tutorial
ALL OF Calculus 2 in 5 minutes
Calculus 2: Applications - Calculating Work (6 of 16) Calculating Work Example 5: Fish Tank
Force and Work of a Spring (Integrals)
Calculus 2: Applications - Calculating Work (9 of 16) Calculating Work Example 8: Trough (Part 1)
Calculus 2: Applications - Calculating Work (13 of 16) Cal. Work Ex. 12: 1/2-Spherical Tank: 1
Finding the Area Between Two Curves by Integration
calculating work, pumping water out of a rectangular tank, calculus 2 tutorial
Комментарии
 0:09:05
0:09:05
 0:09:04
0:09:04
 0:03:30
0:03:30
 0:02:18
0:02:18
 0:06:32
0:06:32
 0:32:06
0:32:06
 0:05:53
0:05:53
 0:57:10
0:57:10
 0:20:55
0:20:55
 0:06:39
0:06:39
 0:08:21
0:08:21
 0:40:37
0:40:37
 0:03:26
0:03:26
 0:08:55
0:08:55
 0:05:24
0:05:24
 0:04:59
0:04:59
 0:11:47
0:11:47
 0:06:09
0:06:09
 0:06:20
0:06:20
 0:03:59
0:03:59
 0:07:50
0:07:50
 0:08:02
0:08:02
 0:07:52
0:07:52
 0:07:36
0:07:36