filmov
tv
Physics 39 Capacitors (24 of 37) Find C for a Spherical Capacitor in 2 Spherical Dielectrics

Показать описание
In this video I will find the capacitance of a spherical capacitor inside 2 spherical dielectrics.
Next video can be seen at:
Physics 39 Capacitors (24 of 37) Find C for a Spherical Capacitor in 2 Spherical Dielectrics
Physics 39 Capacitors (10 of 37) The Spherical Capacitor
Physics 39 Capacitors (22 of 37) Find the Force Needed to Push a Dielectric in a Charged Capacitor
(24-39) Suppose one plate of a parallel-plate capacitor is tilted so it makes a small angle θ with t...
Physics 39 Capacitors (23 of 37) Find C for a Spherical Capacitor in Spherical Dielectric
Physics 39 Capacitors (34 of 37) Gauss' Law and Capacitor with Dielectric
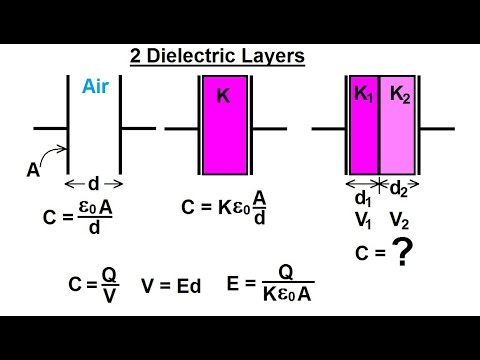
Physics 39 Capacitors (36 of 37) 2 Dielectric Layers
Physics 39 Capacitors (14 of 37) How Does a Dielectric affect a Charged Capacitor?
Physics 39 Capacitors (16 of 37) Final Energy Stored in Capacitor w/ Dielectric
Physics 39 Capacitors (11 of 37) The Isolated Spherical Capacitor
Physics 39 Capacitors (20 of 37) Find C of Capacitor with 4 Dielectrics
Physics - E&M: Ch 39.1 Capacitors & Capacitance Understood (24 of 27) Maximum Charge=?
Physics 39 Capacitors (13 of 37) Placing a Dielectric Inside a Capacitor
Physics 39 Capacitors (12 of 37) Find C of a Capacitor with a Dielectric
Physics 39 Capacitors (18 of 37) Find C when Dielectric is 1/2 way in Capacitor
Physics 39 Capacitors (21 of 37) Find the Force Needed to Push a Dielectric in a Capacitor
Physics 39 Capacitors (25 of 37) Find C Between A and B of a DC-Circuit
Physics 39 Capacitors (33 of 37) Find C, Q, V, U, and t of a Capacitor Circuit
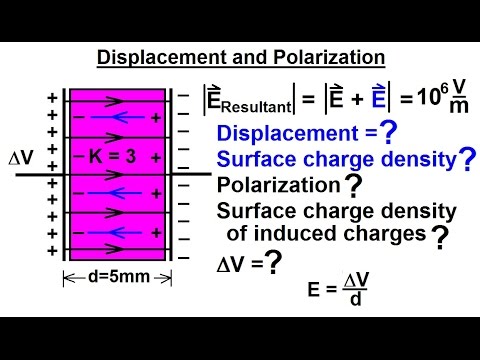
Physics 39 Capacitors (31 of 37) Displacement and Polarization
Physics 39 Capacitors (19 of 37) Find C when a 'Smaller' Dielectric is Inserted
Capacitors in parallel in close analysis
Physics 39 Capacitors (37 of 37) 3 Dielectric Layers
Dielectrics & Capacitors - Capacitance, Voltage & Electric Field - Physics Problems
Physics 39 Capacitors (28 of 37) Find V and C in a DC Circuit with a Switch
Комментарии
 0:08:57
0:08:57
 0:07:25
0:07:25
 0:06:43
0:06:43
 0:03:58
0:03:58
 0:07:03
0:07:03
 0:08:12
0:08:12
 0:06:15
0:06:15
 0:05:27
0:05:27
 0:07:31
0:07:31
 0:05:52
0:05:52
 0:15:53
0:15:53
 0:04:02
0:04:02
 0:08:22
0:08:22
 0:03:45
0:03:45
 0:07:14
0:07:14
 0:08:43
0:08:43
 0:03:39
0:03:39
 0:16:55
0:16:55
 0:09:24
0:09:24
 0:06:41
0:06:41
 0:08:44
0:08:44
 0:03:46
0:03:46
 0:14:19
0:14:19
 0:08:59
0:08:59