filmov
tv
Beyond the Golden Ratio | Infinite Series

Показать описание
You know the Golden Ratio, but what is the Silver Ratio? Learn through active problem-solving at Brilliant:
Dive into more open problem solving right here
Tweet at us! @pbsinfinite
Email us! pbsinfiniteseries [at] gmail [dot] com
RESOURCES
Polygons, Diagonals, and the Bronze Mean by Antonia Redondo
Buitrago
Previous Episode
Proving Brouwer's Fixed Point Theorem
Cut a line segment into unequal pieces of lengths a and b such that the ratio a to b is the same as the ratio (a + b) to a --- that is, so that big over medium equals medium over small. This is how you construct the golden ratio Phi. If a rectangle has an aspect ratio of Phi, you can subdivide it forever into a square and another golden rectangle, and make fun logarithmic spirals by connecting the corners.
Written and Hosted by Gabe Perez-Giz
Produced by Rusty Ward
Graphics by Ray Lux
Assistant Editing and Sound Design by Mike Petrow and Meah Denee Barrington
Special thanks to Roman Pinchuk for supporting us on our Converse level on Patreon.
Along with thanks to Matthew O'Connor, Yana Chernobilsky, and John Hoffman who are supporting us on Patreon at the Identity level!
And thanks to Nicholas Rose, Jason Hise, Thomas Scheer, Marting Sergio H. Faester, CSS, and Mauricio Pacheco who are supporting us at the Lemma level!
Комментарии
 0:14:47
0:14:47
 0:49:49
0:49:49
 0:02:58
0:02:58
 0:07:32
0:07:32
 0:09:46
0:09:46
 0:10:19
0:10:19
 0:18:04
0:18:04
 0:04:18
0:04:18
 0:03:27
0:03:27
 0:00:36
0:00:36
 0:03:20
0:03:20
 0:21:46
0:21:46
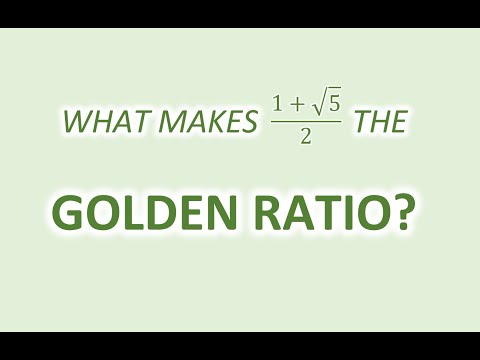 0:08:06
0:08:06
 0:01:34
0:01:34
 0:02:29
0:02:29
 0:03:25
0:03:25
 0:04:47
0:04:47
 0:02:31
0:02:31
 0:04:41
0:04:41
 0:07:10
0:07:10
 0:02:24
0:02:24
 0:03:44
0:03:44
 0:07:00
0:07:00
 0:29:13
0:29:13