Approximating Functions in a Metric Space

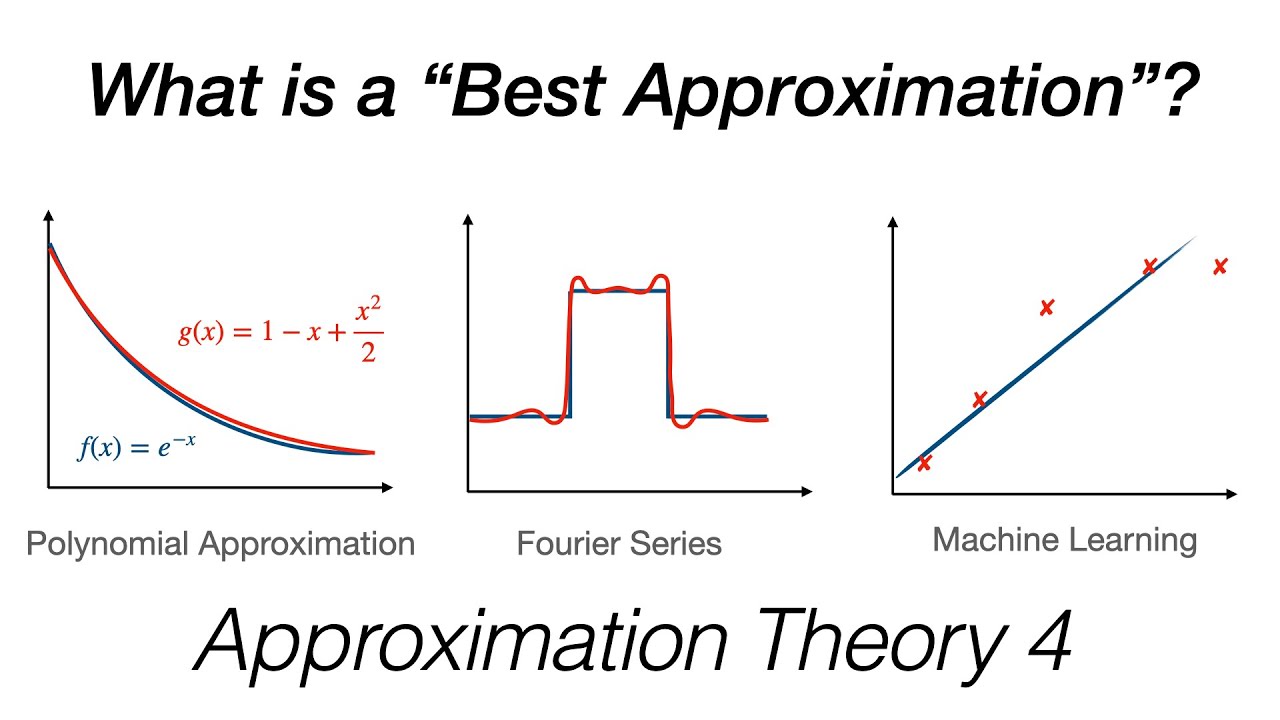
Approximations are common in many areas of mathematics from Taylor series to machine learning.
In this video, we will define what is meant by a best approximation and prove that a best approximation exists in a metric space.

Chapters
0:00 - Examples of Approximation
0:46 - Best Aproximations (definition)
2:32 - Existence proof
7:18 - Summary

The product links below are Amazon affiliate links. If you buy certain products on Amazon soon after clicking them, I may receive a commission. The price is the same for you, but it does help to support the channel :-)

The Approximation Theory series is based on the book "Approximation Theory and Methods" by M.J.D. Powell:

Errata and Clarifications:
A compact subset of a metric space is closed and bounded but a closed and bounded subset of a metric space is not always compact. Please consider the closed versus open set section as illustrative only as the proof strictly requires compactness.

This video was made using:
Animation - Apple Keynote
Editing - DaVinci Resolve

Supporting the Channel.
If you would like to support me in making free mathematics tutorials then you can make a small donation over at
Thank you so much, I hope you find the content useful.

[Zxv]

It's funny, I encountered so many proofs along these lines in my point set topology class and I always found them so dry and hence difficult to follow (or rather, difficult to stay awake long enough to follow them). However, the visuals in this video make it so clear what we're referring to, and the gory details are just there for if you get lost and need some extra structure. Having the visuals as the main proof and the details on the side is delightful, and I really enjoyed this proof. The whole thing seemed borderline obvious, which just goes to show you've done a great job presenting it if your audience is able to guess the conclusion ahead of time.

[geoffrygifari]

I'm used to imagining distance between points but distance between *continuous functions* is completely new

[byronwatkins]

Infinite series are exact equivalents; only truncated series are approximations.

I love the smooth jazz on the background. Makes the learning experience much better, enjoyable and calmer.

[kentgauen]

That existence proof was great. I needed a refresher for my math course. Thanks for sharing!

[gregpetrics]

Great video. Thanks! The theoretical value of a subset being compact in a metric space is hugely under appreciated .

[arsenypogosov]

Function "distance to f" is continuous so by Weierstrass theorem it reaches its infinium on any compact. Q.E.D.

[Tutor-ew]

I promise if you keep pushing with this and find ways to take your brilliant explanations and compound them into some final, cool application you will most certainly blow up. You are so lucid in how you articulate things it's hard to put it into words how things just click when you explain them.

[CristianGarcia]

Enjoyed the video.
As someone who works in ML, its sad to know there exists a best approximation out there but you are stuck with what your model learned.

[mehrdadmohajer]

Thx.
i joined one of the Commentators ( maxwel wilbert) saying : a* is not the good approximation( bc. it is still far away from the point f. if you want to get a good approx. to f, you consider Sub-Space A like a Ballon. As it gets bigger & bigger changes the geometry ( perhaps going from an Appel into a Pear inorder to get as close as possible to f.) At the same time Space B, shrinks toward f, the soulution changes to " minimax " of John v. Newman. Happy to hear more on that from you & the fans.

[edgarbonet]

Also, it would be nice to note that, in this particular case (with the L² norm and A being a vector space), an explicit formula for the best approximation can be derived. It turns out a* is the orthogonal projection of f onto A. It can be computed by projecting f onto an orthogonal basis of A. If the approximation is meant to cover the interval [0,  1], the basis could be the first three shifted Legendre polynomials: 1, 2x−1, and 6x²−6x+1.

See for instance the articles “Orthogonal polynomials” and “Legendre polynomials” on Wikipedia.

[matthewjames]

This is really cool. I'll like the abstract nature of metric space. But how does this help find 'the best approximation' to the function y=e^-x? How could finding a* help in this case?

[mtheory]

So, basically, if you have a set of points on some function, one of them will be closest to some data point from the set of data points you are approximating with that function.

[Maklak]

I think in practical terms, since linear regression minimises the square of distance from data points to approximating function, then a good measure of how good an approximation is would be to integrate the square of difference between a function and its approximation over the finite range we want (a finite Taylor series will shoot out to infinity eventually).

[matveyshishov]

Thank you very much, Will, your videos are so good and easy to understand!!

[tat]

Loving your video Dr. Wood! Great explanations :D

[rektator]

The set of at most degree 2 polynomials is not compact, but do form a closed convex non-empty subset in a Hilbert space of L^2(X) where X is a bounded subset of the some Euclidean space. Therefore these minimizing elements exist.

[rkalle]

In optical applications there are Zernike coefficents describing optical surfaces based on orthogonal polynoms.

[BosonCollider]

Numerically, A being compact is not enough, it also needs to be *located*, i.e. in addition to upper bounds you need to be able to find a lower approximation of the distance from a point to the set in order to find a good approximation of d*. Then this is closely related to Bishop's lemma in constructive analysis

[hypergraphic]

Loving your videos! Keep up the great work