filmov
tv
Integral of ∫csc(x)dx
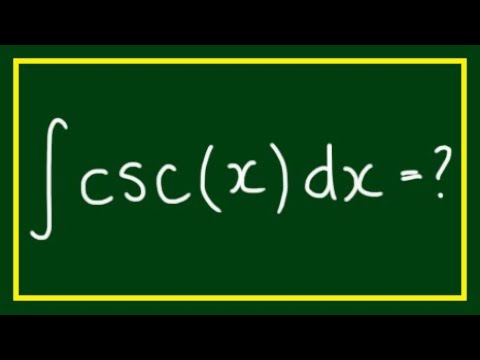
Показать описание
Like the function sec(x), there is no obvious way to integrate csc(x). We need to manipulate csc(x) into an integratable form.
One way is to use the method of partial fractions. While this method takes a quite a few steps to solve the integral, it is robust.
Using the method of partial fractions, the idea is to rewrite the integral of csc(x) as:
∫csc(x)dx = ∫sin(x)dx / (1 - cos^2(x))
Then by letting u = cos(x)...
∫csc(x)dx = -∫du / (1 - u^2)
We can then convert the expression 1/(1+u)(1-u) into the sum of its partial fractions.
Another way involves some trickery where we try to form an integral of the form f'(x)/f(x), which gives the result ln|f(x)|. Although this method is efficient, it requires you to know part of the answer before you begin, which doesn't make much sense.
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
One way is to use the method of partial fractions. While this method takes a quite a few steps to solve the integral, it is robust.
Using the method of partial fractions, the idea is to rewrite the integral of csc(x) as:
∫csc(x)dx = ∫sin(x)dx / (1 - cos^2(x))
Then by letting u = cos(x)...
∫csc(x)dx = -∫du / (1 - u^2)
We can then convert the expression 1/(1+u)(1-u) into the sum of its partial fractions.
Another way involves some trickery where we try to form an integral of the form f'(x)/f(x), which gives the result ln|f(x)|. Although this method is efficient, it requires you to know part of the answer before you begin, which doesn't make much sense.
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
integral of csc(x), the standard result, calculus 2 tutorial
Integrals#13 ~ Integral csc x dx ~ Like You've Never Seen It Before...W/Cray-cray Substitution ...
Integral of csc(x), without that trick!
integral of csc x dx
Integral of csc(x)
Integral of cscx | Integration of cosecant x
Why the integral of csc x has 'different' solutions
Integral of csc(x) via Weierstrass substitution
Calculus 2 Exam Review Part6
integral cscx dx integral csc^2x dx
Integral of ∫csc(x)dx
Integral of csc x dx
integral of csc x cot x dx
INTEGRAL of csc(x) that makes sense
Integral of csc x ❖ Calculus 1 ❖ Trig Integrals
Integral of csc(x)sec(x)
Solving Integral: ∫ csc x / √x dx
integral of csc(x), Weierstrass Substitution
Integral of csc(x)*(cot(x) - csc(x))
Integral of Csc(x) In two Different Ways!
Integrate ∫5/csc(x) dx
Integrating Cosec(x) | csc(x)dx
Integral of csc^4(x)csc(x)cot(x)
INTEGRAL DE csc(x) - CAMBIO DE VARIABLE (SUSTITUCIÓN)
Комментарии
 0:03:46
0:03:46
 0:01:08
0:01:08
 0:04:00
0:04:00
 0:03:08
0:03:08
 0:02:36
0:02:36
 0:03:00
0:03:00
 0:17:44
0:17:44
 0:00:47
0:00:47
 5:47:36
5:47:36
 0:08:07
0:08:07
 0:03:22
0:03:22
 0:02:02
0:02:02
 0:04:18
0:04:18
 0:04:18
0:04:18
 0:00:29
0:00:29
 0:00:57
0:00:57
 0:01:34
0:01:34
 0:02:10
0:02:10
 0:16:20
0:16:20
 0:02:16
0:02:16
 0:08:33
0:08:33
 0:02:37
0:02:37
 0:03:53
0:03:53