filmov
tv
Integral of csc(x), without that trick!

Показать описание
integral of csc(x) without that trick!,
integrals by student: Chase Snidfar,
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
integrals by student: Chase Snidfar,
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Integral of csc(x), without that trick!
integral of csc(x), the standard result, calculus 2 tutorial
Integral of csc(x) via Weierstrass substitution
Why the integral of csc x has 'different' solutions
integral cscx dx integral csc^2x dx
Integral of csc(x)
Integrals#13 ~ Integral csc x dx ~ Like You've Never Seen It Before...W/Cray-cray Substitution ...
Integral of csc(x)sec(x)
Calculus 2 Exam Review Part6
An unorthodox method of solving the Integral of csc(x)
Integral of sec(x) & integral of csc(x), the usual trick
Integrating Cosec(x) | csc(x)dx
INTEGRAL of csc(x) that makes sense
Integral of (csc(x))^3(sec(x))
Integral of csc(x)
Integral of Csc(x) In two Different Ways!
Integral of 1/Sin(x) aka Csc(x) : Easiest way to compute
Integral of csc(x)
Integral of csc x ❖ Calculus 1 ❖ Trig Integrals
integral of csc(x), Weierstrass Substitution
Integral of -csc(x)cot(x)/sqrt(100 - csc^2(x))
when calculus students use trig identities too early
Integral of sec(x)csc(x) dx (Integral of trigonometric functions)
integral of csc x dx
Комментарии
 0:04:00
0:04:00
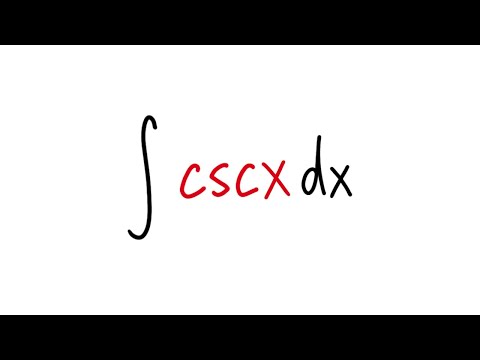 0:03:46
0:03:46
 0:00:47
0:00:47
 0:17:44
0:17:44
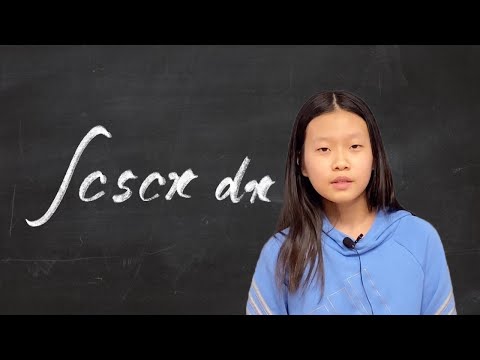 0:08:07
0:08:07
 0:02:36
0:02:36
 0:01:08
0:01:08
 0:00:29
0:00:29
 5:47:36
5:47:36
 0:08:33
0:08:33
 0:04:41
0:04:41
 0:08:33
0:08:33
 0:04:18
0:04:18
 0:01:38
0:01:38
 0:04:58
0:04:58
 0:16:20
0:16:20
 0:05:57
0:05:57
 0:02:05
0:02:05
 0:04:18
0:04:18
 0:01:34
0:01:34
 0:02:44
0:02:44
 0:00:43
0:00:43
 0:01:31
0:01:31
 0:03:08
0:03:08