filmov
tv
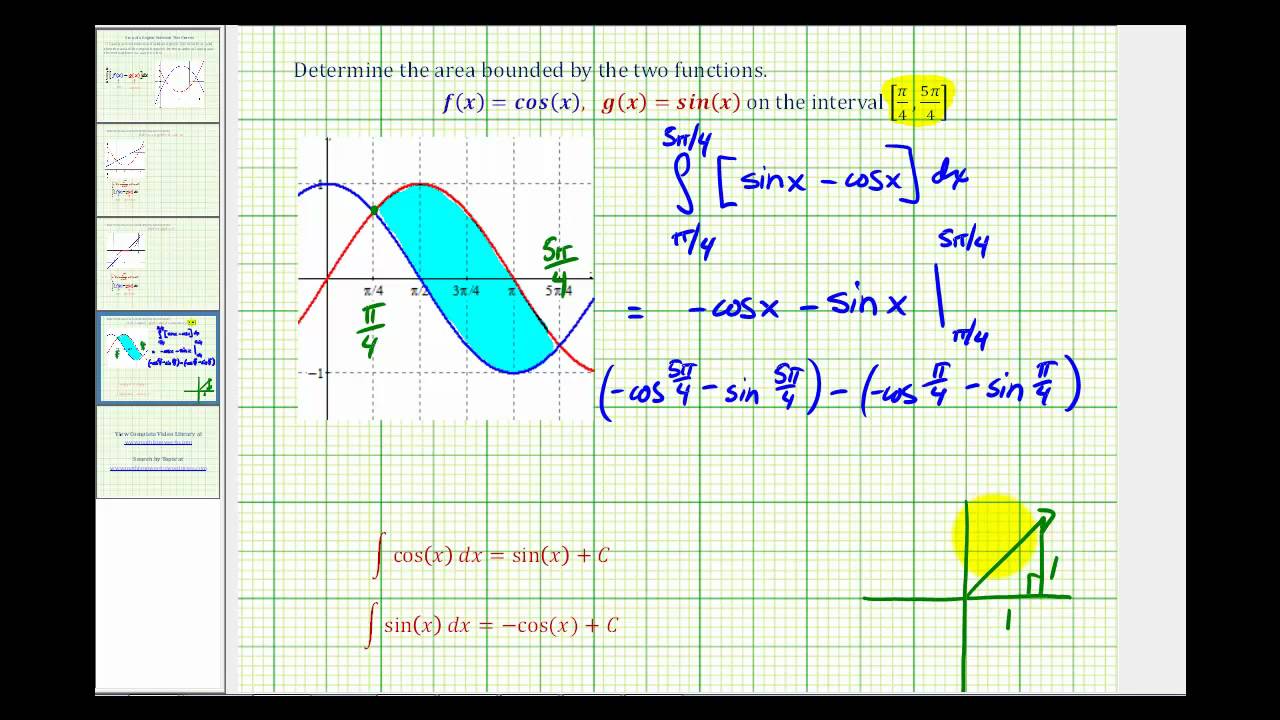
Ex 3: Area Bounded by Two Trig Functions
Показать описание
This video provides an example of how to determine the area bounded by two trigonometric functions.
Ex 3: Area Bounded by Two Trig Functions
Area of a Region Bounded by 3 Curves (Calculus)
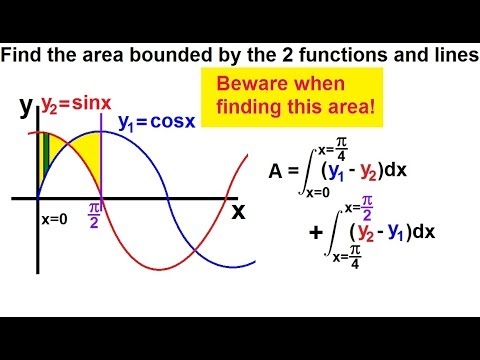
Calculus 2 - Integration: Finding the Area Between Curves (3 of 22) Ex. 3: y=sinx, y=cosx BEWARE!
Area Between Two Curves
Ex 3: Find Area Between Two Exponential Functions (respect to x)
Calculus II: Area of the region bounded by three curves
Find the area enclosed by the two curves
Finding the Area Between Two Curves by Integration
Find area of region bounded by curves y = x^3 - 3x^2 +2x and y =0, x=3. Areas in the Plane
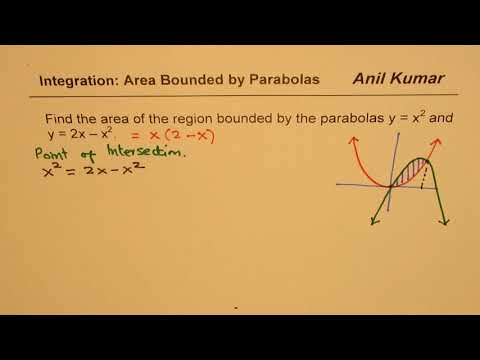
Find Area of region bounded by parabolas Integration AP Calculus
Calculus - Integration: Volume by Rotating an Area (3 of 10) Ex. 3: y=x^2,y=x About the x-axis
How to Solve Area Bounded By Curves Using Integral Calculus
Calculus 2: Polar Coordinates (22 of 38) Area Bounded by a Polar Curve Ex 3
Applications of Integration: Area Bounded by three curves
Calculus Integration Area Between the Curves IB Math HL
Area bounded by y = x and y = x^3
AREA BOUNDED BY THE CURVE AND THE LINE || STEP BY STEP METHOD
Trying transition video for the first time 💙😂 || #transformation #transition #shorts #viralvideo...
M204 Sec10_3 Area of Regions bounded by Polar Curves - Ex 3
Ex 4: Find Area Between Two Quadratic Functions (respect to x)
Ex: Find the Area of a Triangle Bounded by a Line, a Perpendicular Line, and the Y-Axis
Sketch and find area bounded by region of graph y = x^3 -3x^2 +2x and the x-axis. Definite Integral
How to Find the Area Bounded by the Graphs of y = 3^x, y = 0, x = 0, x = 4
IIT Bombay CSE 😍 #shorts #iit #iitbombay
Комментарии
 0:03:56
0:03:56
 0:07:35
0:07:35
 0:08:43
0:08:43
 0:48:59
0:48:59
 0:04:36
0:04:36
 0:07:53
0:07:53
 0:07:09
0:07:09
 0:07:52
0:07:52
 0:07:12
0:07:12
 0:05:59
0:05:59
 0:07:30
0:07:30
 0:13:32
0:13:32
 0:06:03
0:06:03
 0:05:13
0:05:13
 0:07:23
0:07:23
 0:02:21
0:02:21
 0:16:06
0:16:06
 0:00:15
0:00:15
 0:07:19
0:07:19
 0:05:42
0:05:42
 0:05:22
0:05:22
 0:05:05
0:05:05
 0:02:15
0:02:15
 0:00:11
0:00:11