filmov
tv
Infinite Geometric Series Sum
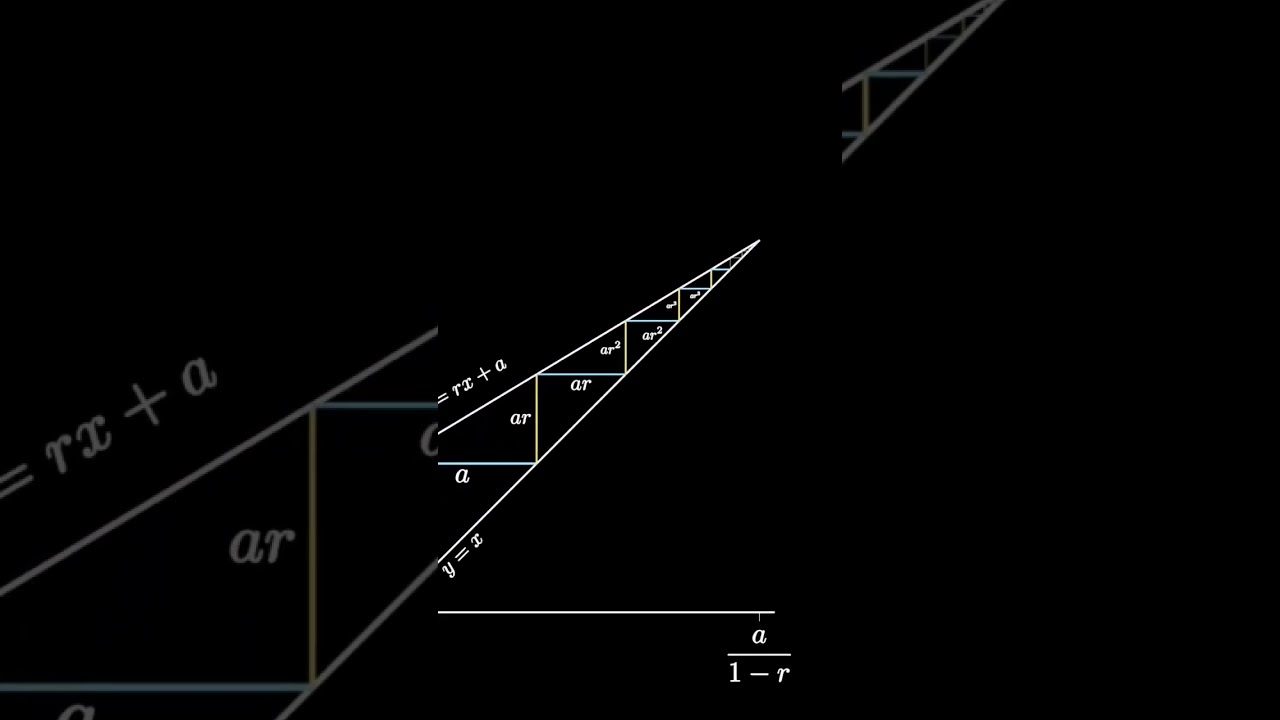
Показать описание
This is a short, animated visual proof demonstrating the infinite geometric series formula for any positive ratio r with r less than 1 and with positive first term a. This series is important for many results in calculus, discrete mathematics, and combinatorics.
#mathshorts #mathvideo #math #calculus #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #geometricsums #series #infinitesums #infiniteseries #geometric #geometricseries
To learn more about animating with manim, check out:
#mathshorts #mathvideo #math #calculus #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #geometricsums #series #infinitesums #infiniteseries #geometric #geometricseries
To learn more about animating with manim, check out:
Finding The Sum of an Infinite Geometric Series
Sum of an infinite geometric series | Sequences, series and induction | Precalculus | Khan Academy
Infinite Geometric Series Sum
Infinite Geometric Series Sum
Sum of Infinite Geometric Series
Visual proof of infinite geometric series sum
Infinite Sums | Geometric Series | Explained Visually
How to determine the sum of a infinite geometric series
Another derivation of the sum of an infinite geometric series | Precalculus | Khan Academy
sum of an infinite geometric series
Infinite Geometric Series | Sum to Infinity
Learning how to find the sum of an infinite geometric series
Visual proof of infinite geometric series sum II
Edexcel A Level Maths: 3.5 Sum to Infinity (Geometric Series)
Sum to Infinity | Geometric Series | Explain in Detailed |
Infinite geometric series [IB Maths AA SL/HL]
Ex 1: Find the Sum of an Infinite Geometric Series
INFINITE GEOMETRIC SERIES || GRADE 10 MATHEMATICS Q1
Learn how to find the sum of an infinite geometric series in summation notation
Infinite Geometric Series I Señor Pablo TV
Computing the Sum of an Infinite Geometric Series: Sum( 2*(1/3)^n, n = 3, 4, ...)
A visual infinite sum like you’ve never seen!
What's this infinite sum?
[Tagalog] Sum of Infinite Geometric Sequence #Infinite #Math10 #Firstquarter
Комментарии
 0:19:50
0:19:50
 0:04:46
0:04:46
 0:00:45
0:00:45
 0:01:00
0:01:00
 0:03:36
0:03:36
 0:01:41
0:01:41
 0:02:47
0:02:47
 0:03:41
0:03:41
 0:07:54
0:07:54
 0:00:11
0:00:11
 0:05:21
0:05:21
 0:02:08
0:02:08
 0:01:41
0:01:41
 0:08:30
0:08:30
 0:23:42
0:23:42
 0:10:31
0:10:31
 0:03:45
0:03:45
 0:13:58
0:13:58
 0:02:06
0:02:06
 0:04:33
0:04:33
 0:02:04
0:02:04
 0:00:57
0:00:57
 0:00:31
0:00:31
![[Tagalog] Sum of](https://i.ytimg.com/vi/g2SRc1VUfno/hqdefault.jpg) 0:08:03
0:08:03