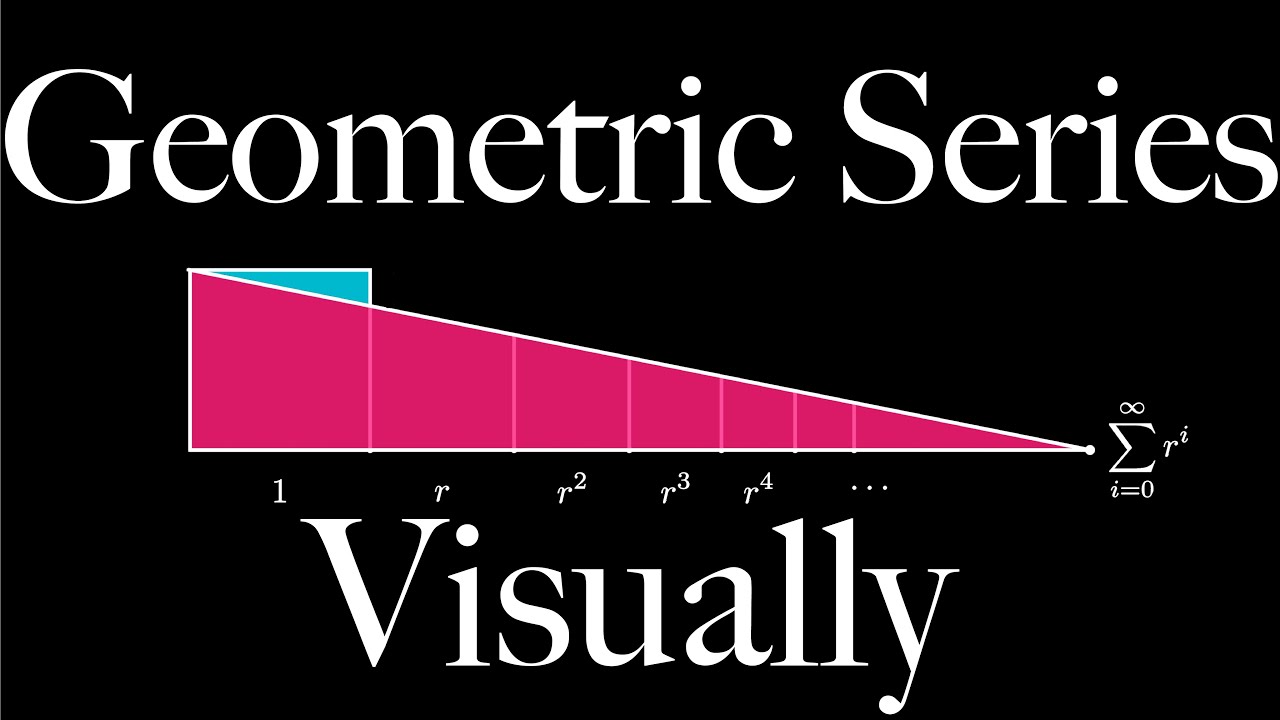
Visual proof of infinite geometric series sum

This is a short, animated visual proof demonstrating the infinite geometric series formula for any positive ratio r with r less than 1. This series is important for many results in calculus, discrete mathematics, and combinatorics. #mathshorts​ #mathvideo​ #math​ #calculus #mtbos​ #manim​ #animation​ #theorem​ #pww​ #proofwithoutwords​ #visualproof​ #proof​ #iteachmath #geometricsums #series #infinitesums #infiniteseries #geometric #geometricseries

If you like this content, please consider subscribing.

To learn more about animating with manim, check out:

______________________________
Music in this video:
Addicted by VYEN

[mathflipped]

This is such a clean visualization! Amazing proof, and great job on the video!

[quadrannilator]

Very neat, using geometry to make a proof of geometric series.
The only additional caption I'd like to add is that while making the hypotenuse of the bigger triangle, you could show that the same line has to pass through all the vertical column points by virtue of slope & intercept equivalence and also therefore be a convergent sum.
Loved learning of this way to see this sum.

[mutercimcime]

this is by far the coolest proof I've ever seen in my life

[PeterBarnes]

I would maybe reorganize the proof a little. Make a trapezoid segment as shown with vertical side lengths of 1 and r, construct the small triangle and then the larger similar triangle, then show that a similar trapezoid may be produced in the large triangle with vertical side lengths r and r^2, and that repeating the same triangle construction with the new trapezoid produces a new large triangle which must be contained in the first large one because it is similar. That should essentially complete the inductive proof in this visual manner.

[NuridinYumer]

Now I understand, thank you very much for that.

[oliverfrancescoriccetti]

I have a doubt. You constructed the horizontal line as the sum of the powers of r. And you made it finite. So it converges. But isn’t this what you want to prove?

[Kyagundabanegaratu]

Why its not curved shape but a triangle? Pls explain

[Vannishn]

Oh I'm going to show this to the kids I teach ! Amazing not having to go through the formal inverse of 1 + x + x^2 + … Thank you !

[tusharsachdeva]

when i used to do math in school, it was so difficult to solve a problem analytically. then i would create a diagram from the problem description and the solution would just be apparent and it became so easy that it felt wrong. i don't understand why are elementary problems solved analytically. just solve them through geometry or through numpy or something. math is made so difficult in schools.

[erebus-pi]

If the infinite geometric series converge, is |r| < 1?

[nathanielbrock]

I like the proof but I don't see why this would construct a triangle and not some sort of curved shape.

[MaxG]

Why must the two triangles be similar?

[NdrXbrain]

Nice, btw, I'll talk about Geometric sequences in my participation to #SoME2, if I completed the video making,