filmov
tv
Unique Exponential Equation | How To Solve The Exponential Equation Problem | Aman Sir

Показать описание
Today we will Solve a Unique Exponential Equation, which will surprise you.
In this video, we will discuss the exponential equation problem and we will learn how to solve the unique exponential equation.
this exponential equation is picked from an exam from Russia, and also these types of problems are often asked in JEE advanced exam.
This question is a good revision of JEE Advanced level Exponential equation question & will surely help you learn good concepts of the Exponential equation.
Let's see the simplistic solution by Aman sir to this Unique Exponential Equation.
so watch this full video and learn how to solve these types of exponential equations and what type of concept and method we will use to solve this exponential equation.
Solve This Exponential Problem
🚀🚀Social Media Links:🚀🚀
----------------------------------------------------------------------------------------
Telegram Handle: @bhannatmaths @bhannatmathsofficial
----------------------------------------------------------------------------------------
#amansirmaths #bhannatmaths #maths #exponential #exponentialequations
For All Notifications Join Our Telegram Group: @bhannatmaths
In this video, we will discuss the exponential equation problem and we will learn how to solve the unique exponential equation.
this exponential equation is picked from an exam from Russia, and also these types of problems are often asked in JEE advanced exam.
This question is a good revision of JEE Advanced level Exponential equation question & will surely help you learn good concepts of the Exponential equation.
Let's see the simplistic solution by Aman sir to this Unique Exponential Equation.
so watch this full video and learn how to solve these types of exponential equations and what type of concept and method we will use to solve this exponential equation.
Solve This Exponential Problem
🚀🚀Social Media Links:🚀🚀
----------------------------------------------------------------------------------------
Telegram Handle: @bhannatmaths @bhannatmathsofficial
----------------------------------------------------------------------------------------
#amansirmaths #bhannatmaths #maths #exponential #exponentialequations
For All Notifications Join Our Telegram Group: @bhannatmaths
Комментарии
 0:12:45
0:12:45
 0:05:58
0:05:58
 0:00:56
0:00:56
 0:08:18
0:08:18
 0:03:31
0:03:31
 0:09:51
0:09:51
 0:04:05
0:04:05
 0:00:25
0:00:25
 0:00:23
0:00:23
 0:10:06
0:10:06
 0:16:36
0:16:36
 0:00:54
0:00:54
 0:11:47
0:11:47
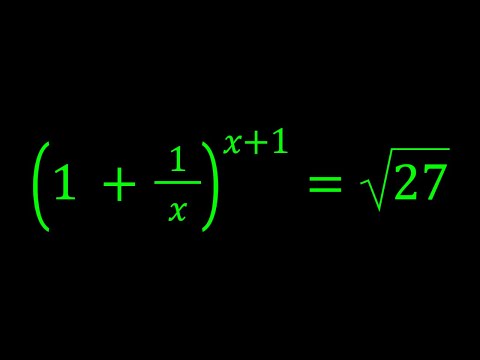 0:08:37
0:08:37
 0:03:33
0:03:33
 0:00:22
0:00:22
 0:11:08
0:11:08
 0:09:15
0:09:15
 0:00:28
0:00:28
 0:01:39
0:01:39
 0:09:39
0:09:39
 0:00:26
0:00:26
 0:00:40
0:00:40
 0:08:47
0:08:47