filmov
tv
can you solve this exponential equation?

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
can you solve this exponential equation?
Germany | Can you solve this? | Exponential Olympiad Mathematics.
Spain l can you solve this?? l Olympiad Math Radical Exponential Problem
Can you solve this? | Exponential Equation | Algebra Problem.
USA| A Tricky Math Olympiad Exponential Equation. Can you solve? #algebra
Germany l can you solve?? l Olympiad Math exponential problem
Can you solve this exponential equation? – Math tutorial😏😶
Can You Solve This | A Challenging Exponential Equation
Can You Solve this Math Olympiad Problem | Exponential equation |
A Beautiful Exponential Equation | Can You Solve This?
Can You Solve this Exponential Equation? | Step-by-Step Explanation
Can you solve this exponential equation without a calculator?
A Challenging Exponential Equation | Can You Solve This?
Can you solve this? | Math Puzzle
Germany l can you solve this?? l Olympiad Math exponential problem
Can You Solve An Exponential Equation?
Solving Exponential Equation
Germany | Can you solve this? | A Nice Olympaids Exponential Trick.!!
Exponential Equations - Algebra and Precalculus
The Ultimate Math Olympiad Challenge: Can You Solve This Exponential Problems?
Russian l can you solve this exponential problem?? l Olympiad Mathematics
A Challenging Exponential Equation | Can You Solve This?
How to solve this exponential equation without a calculator
A Challenging Exponential Equation | Can You Solve This?
Комментарии
 0:12:45
0:12:45
 0:04:12
0:04:12
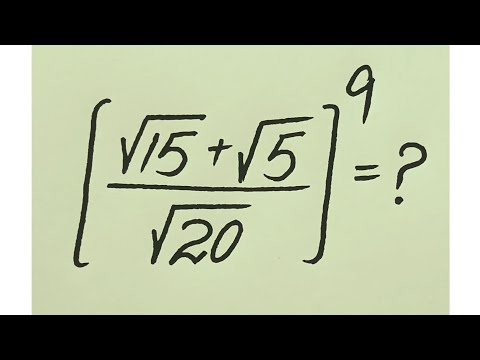 0:15:10
0:15:10
 0:03:33
0:03:33
 0:08:19
0:08:19
 0:09:59
0:09:59
 0:05:17
0:05:17
 0:16:06
0:16:06
 0:06:31
0:06:31
 0:06:03
0:06:03
 0:10:34
0:10:34
 0:14:34
0:14:34
 0:12:02
0:12:02
 0:13:51
0:13:51
 0:17:05
0:17:05
 0:08:21
0:08:21
 0:00:56
0:00:56
 0:12:10
0:12:10
 0:05:58
0:05:58
 0:04:18
0:04:18
 0:15:12
0:15:12
 0:12:45
0:12:45
 0:14:18
0:14:18
 0:11:08
0:11:08