filmov
tv
Proof that (R, +) is not a Cyclic Group

Показать описание
Proof that (R, +) is not a Cyclic Group.
We prove that the set of real numbers under the operation of addition does not form a cyclic group. This is really an easy observation but in this video we go through the details.
We prove that the set of real numbers under the operation of addition does not form a cyclic group. This is really an easy observation but in this video we go through the details.
Proof that (R, +) is not a Cyclic Group
S01.9 Proof That a Set of Real Numbers is Uncountable
An Example Proof using Identities of Regular Expressions
Proof that r squared is correlation coefficient squared
Proof and Problem Solving - Relations Example 06
Proof: Archimedean Principle of Real Numbers | Real Analysis
Proof and Problem Solving - Relations Example 02
Proof: Product of Absolute Values is the Absolute Value of the Product
payrib withdrawal proof | how to withdraw in payrib | live proofhttps://payrib.com/?r=300551
What is Combinatorial Proof ? Why C(n, r) = C(n, n-r) ? : a Combinatorial proof | Part - 1
Vector Spaces 2: Proof that R over Q is of infinite dimension
Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Proof and Problem Solving - Relations Example 03
Mathematical Induction - Proof of ∑r=n(n+1)/2 | ExamSolutions
Proof by Induction : Sum of series ∑r² | ExamSolutions
Proof of Binomial Coefficients to follow Pascals Triangle
Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Proof of the sum of r^2 series
Proof of V E + R = 2
Triangle Area from Inradius and Semiperimeter (visual proof)
Proof the Area of a Circle is Pi R squared. (In about a minute)
Proof of R is not Compact | L3 | Compactness @ranjankhatu
Proof that (n choose r) equals (n choose (n-r) )
Important Math Proof: The Set of Equivalence Classes Partition a Set
Комментарии
 0:04:05
0:04:05
 0:04:02
0:04:02
 0:05:49
0:05:49
 0:03:24
0:03:24
 0:04:14
0:04:14
 0:06:26
0:06:26
 0:04:13
0:04:13
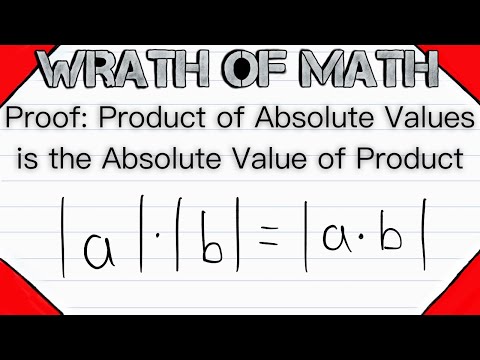 0:05:15
0:05:15
 0:03:21
0:03:21
 0:05:59
0:05:59
 0:16:24
0:16:24
 0:04:19
0:04:19
 0:03:48
0:03:48
 0:08:13
0:08:13
 0:08:16
0:08:16
 0:05:56
0:05:56
 0:04:46
0:04:46
 0:06:29
0:06:29
 0:04:18
0:04:18
 0:01:56
0:01:56
 0:01:31
0:01:31
 0:18:05
0:18:05
 0:03:46
0:03:46
 0:07:15
0:07:15