filmov
tv
Solving a Diophantine equation|Use a simple trick to find the roots
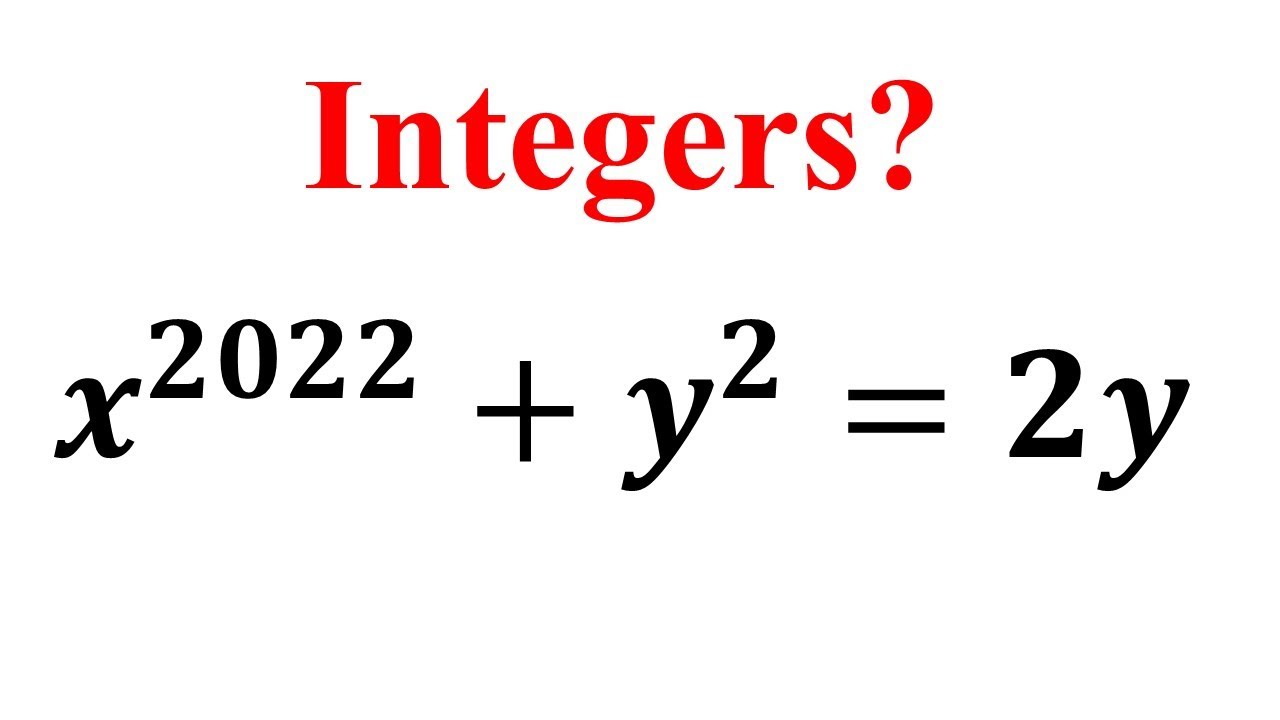
Показать описание
Diophantine Equation: ax+by=gcd(a,b) ← Number Theory
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
A Linear Diophantine Equation
A Linear Diophantine Equation | 3x+4y=17
Diophantine Equations: Strategies and Examples
A Linear Diophantine Equation
Solving Linear Diophantine Equations - Simplified
A Great Book on Diophantine Equations
New Method To Solve Linear Diophantine Equation | asH maths
How to solve Diophantine Equations - ISI BSTAT BMATH / Pre-RMO
How to Solve a Diophantine Equation | Integer Solutions?
Using the Euclidean Algorithm to solve a linear Diophantine equation
A Radical Diophantine Equation | #math #numbertheory
Solving A Diophantine Equation
Solving a Quadratic Diophantine Equation
A Diophantine Equation @dhdkro
A Diophantine Equation | a^2=b^2+13
I Solved An Exponential Diophantine Equation
A Special Diophantine Equation in Number Theory with Special Formula You Need to Master
A Diophantine Equation | a^2+b^2=715
Solving A Set Of Diophantine Equation In Under A Minute
A Diophantine Equation with Integer Solutions
Number Theory | Linear Diophantine Equations
Solve Diophantine Equation by Factoring
Комментарии
 0:09:43
0:09:43
 0:07:40
0:07:40
 0:00:27
0:00:27
 0:00:47
0:00:47
 0:27:34
0:27:34
 0:10:24
0:10:24
 0:13:16
0:13:16
 0:00:18
0:00:18
 0:01:00
0:01:00
 0:23:16
0:23:16
 0:08:58
0:08:58
 0:03:26
0:03:26
 0:00:28
0:00:28
 0:09:24
0:09:24
 0:11:04
0:11:04
 0:14:11
0:14:11
 0:00:46
0:00:46
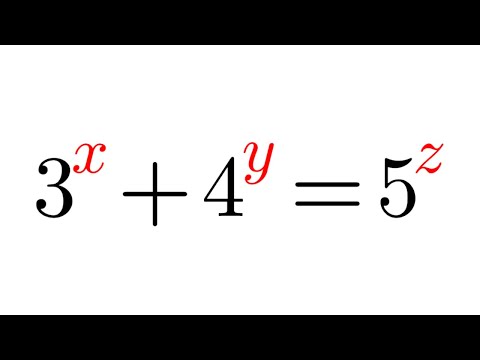 0:11:12
0:11:12
 0:08:10
0:08:10
 0:00:40
0:00:40
 0:00:58
0:00:58
 0:00:49
0:00:49
 0:09:17
0:09:17
 0:00:35
0:00:35