Gravitational Potential is NOT mgh!!!

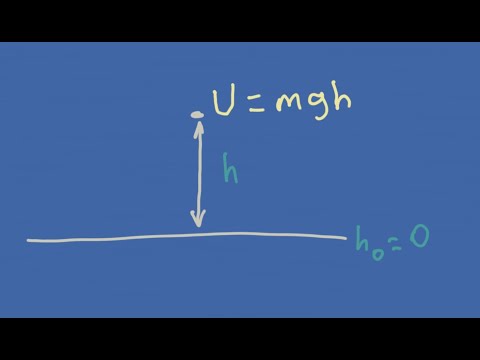
Here we derive and explore the true Gravitational Potential Energy of an object within a gravitational field. Gravitational Potential Energy (Ug , GPE or PEG , depending on who you ask) is only approximated as mgh when it in fact is not. So here we use Newton's Law of Universal Gravitation to along with the definition of Work to integrate to get the potential energy of an object.

It is important to point out that when using this potential energy function the potential is zero only at an infinite radius. All other radii have negative potentials.

Additionally it is important to point out, that for any object at a nonzero radius from another object, the potential energy of the object is finite. So even if you lift something infinitely high, you will only ever do so much work on that object. This leads to escape velocity, which we will explore in another video.

[jordan]

came from your hohmann transfer looking through a par-e light problem I was having.... I was throwing be-borlie, hisinberg, boltsman and showdinnger lol. but this and your vid on hohman transfer really helped

[brendanfan]

in your video, there 2 potential energy formulas: U=mgh and U=-GMm/r. you should show your reader that, the first one is based on setting the surface of the earth as zero point, (of course, it is approximate as it uses g = GMm/R2 to replace GMm/(R+h)xR while the second one set zero at infinity far. This is the key point of the calculation.

[graduxx]

so basically it’s Fg.h but h is r and Fg is the Newton’s law form Fg = -GMm/r2 and so Ug = -GMm/r right ? no need to use integral or stuff