filmov
tv
Modular Inverses in Python 3 (PicoCTF 2022 #03 basic-mod2)

Показать описание
Help the channel grow with a Like, Comment, & Subscribe!
Check out the affiliates below for more free or discounted learning!
📧Contact me! (I may be very slow to respond or completely unable to)
Check out the affiliates below for more free or discounted learning!
📧Contact me! (I may be very slow to respond or completely unable to)
Modular Inverses in Python 3 (PicoCTF 2022 #03 basic-mod2)
How To Find The Inverse of a Number ( mod n ) - Inverses of Modular Arithmetic - Example
Modular Inverse - Fermats Little Theorem [Python] Math
Modulo Multiplicative Inverse (with Python Implementation)
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Python - Exponents, Modular Exponents, Modular Inverse Tutorial
Python :Modular multiplicative inverse function in Python(5solution)
Multiplikatives Inverses modulo berechnen (Beispiel 1)
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
How much does a PHYSICS RESEARCHER make?
COC4010_1.19_Crypto Maths3 _Galois Fields_Modular Polynomial Arithmetic
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Modulo Operator Examples #Shorts #math #maths #mathematics #computerscience
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
Modular Multiplicative Inverse - Cryptography - Cyber Security - CSE4003
Code Review: Python extended Euclidean algortihm + inverse modulo
How much does B.TECH pay?
Modular Inverse - Fermats Little Theorem [C++] Math
Learn Python by Exercises #7: The Inverse Case
What is Modular Inverse and How to Find it!?? [Tutorial]
Python dictionaries are easy 📙
Python Tutorial: Inverse Dynamics of 3-Link RRR Articulated Arm using SymPy and NumPy
L11-How to Quickly Compute Modular Multiplicative Inverse
Modular inverse and Inverse Factorial
Комментарии
 0:10:21
0:10:21
 0:10:58
0:10:58
 0:01:37
0:01:37
 0:17:01
0:17:01
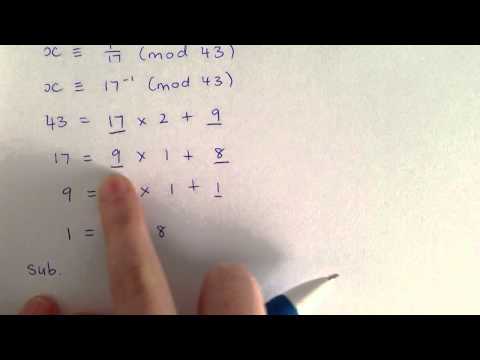 0:06:00
0:06:00
 0:43:49
0:43:49
 0:03:37
0:03:37
 0:11:09
0:11:09
 0:22:21
0:22:21
 0:00:44
0:00:44
 0:24:11
0:24:11
 0:00:16
0:00:16
 0:00:30
0:00:30
 0:00:20
0:00:20
 0:15:14
0:15:14
 0:01:37
0:01:37
 0:00:34
0:00:34
 0:02:50
0:02:50
 0:04:11
0:04:11
 0:08:05
0:08:05
 0:08:06
0:08:06
 0:26:16
0:26:16
 0:25:01
0:25:01
 0:07:55
0:07:55