Find All Possible Values - a Problem of Divisors | Number Theory | Viewer Suggested Problem

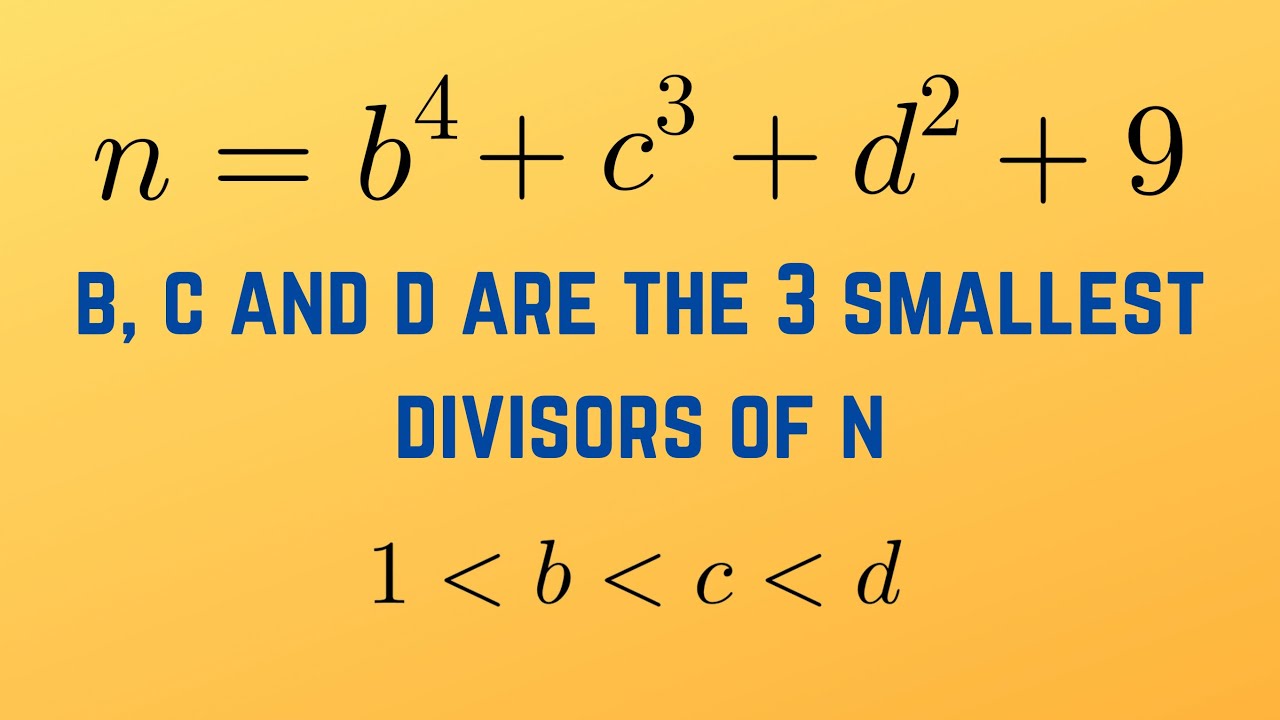
Показать описание

This is a nice number theory problem sent in by a viewer.

b, c and d are the three smallest positive divisors of n, not equal to 1.
Also, n = b⁴ + c³ + d² + 9.
Can you find all possible values of n?

Did you solve it?
Let me know in the comments how you solved this problem. I’d love to hear about it!

Test your friends and family to see if they're as quick as you.
Challenge yourself to fun and interesting maths problems and start your journey as an olympiad.
Maths videos by Giuliano Grasso - mathematics graduate from the University of East Anglia.

I post weekly maths olympiad videos for you to try and solve.

If you want to see more problems or send me your own, then subscribe here:

Рекомендации по теме

Комментарии

Just want to add, at 0:18 I should have made it clearer that b must also be odd.

And at 1:07, d^2 is just 1 mod 4.

GGMaths

nice i like this problem because it involves divisors, never seen in this channel.

timetraveller

I remember that on a turkish contest "Antalya Math Olympiad" this problem was featured either 2017 or 2018. Nice solution btw !

asmocak

Do you have any video for mod equations??
Anyway, it's

samihaafsaraibnat

Yay ! The reason why I like problems involving divisors is because they use more common sense than Number Theory 😁
And your solution was very ingenious ! I liked it ! And once again thanks for mentioning me in the video, lol 😂

srijanbhowmick

Let n be a positive integer. Show that any number greater than n⁴/16 can be written in at most one way as the product of two of its divisors having difference not exceeding n.

(1998 St. Petersburg City Mathematical Olympiad)

Please solve this one on your channel .
Thanks.

TechToppers

2:29 "...plus 2p all squared..." but you write 8p^2. This doesn't affect the result, but it is a weird typo.

themathhatter

Find All Possible Values - a Problem of Divisors | Number Theory | Viewer Suggested Problem

Find the sum of all possible values of x² + y²

Find All Possible Values - a Problem of Divisors | Number Theory | Viewer Suggested Problem

Find all possible values of X | Triangle Inequality Theorem | Important math skills explained

Find all possible values of X | Solving Inequalities | Important math skills explained

15 Possible values for expression

Find All Possible Values of M | Azerbaijani Olympiad | Number Theory | Math Olympiad Training

16 Possible values for t

Find all possible values of x in this nice exponential function question

Day 2 - Bi-Annual Planning and Work Session- State Board of Education - Dec. 4, 2024

Identify the set of possible values for each random variable.

Find the values a and b that make the piecewise function continuous

13 Possible values for x

Find all possible values of coefficient for Factorable Trinomial

Find all possible values of θ, where 0^∘ ≤θ≤360^∘. cosθ=-…

Russian l Very Nice Olympiad Math Problem l Find all possible values of k?

Find The Values of n | Number Theory | Math Problem Solving

Find all possible values of θ, where 0^∘ ≤θ≤360^∘. cosθ=-1

Finding All Values of a Such That There Are No x- and y-Intercepts for f(x) = 2| x + 1| + a

Find all possible values of x for which the number 7x3 is divisible by 3 Also find each such number

Find all the possible values of x for similar triangles

Finding all possible values of the inverse sine of a given value

For each of the following, find all possible values of the scalar αthat make the matrix defec…

Find Possible Values of X & Y | A Nice Algebraic Problem

Find all possible values of (a) L,(b) L_2, and (c) θfor a hydrog…