filmov
tv
Find the sum of all possible values of x² + y²

Показать описание
This problem is from the Harvard-MIT Mathematics Tournament.
What is the sum of 3/4 and 2/3?
How to find the sum of 3 numbers
Math tutorial for determining the sum of an arithmetic series
Finding The Sum of an Infinite Geometric Series
Finding the sum or an arithmetic series using summation notation
Find the sum of all multiples of 3 between 1 and 1000. Arithmetic Series
ARITHMETIC SEQUENCE: FINDING THE SUM OF ALL ODD INTEGERS.
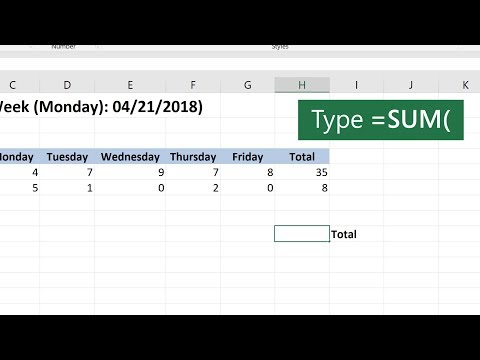
How to Use Sum Function in Excel
Find the sum of all prime factors of 1998 #primefactorisation #fyp
Find the sum of the following fractions
Sum of an Arithmetic Sequence: Find the sum of multiples
Arithmetic Series - Sum of the Terms of Arithmetic Sequence
ARITHMETIC SEQUENCE: SUM OF ALL EVEN NUMBERS
Find the Sum of the Even Integers Between 39 and 101
How To Find All Combinations That Equal A Given Sum In Excel
How to find the sum of a mixed number and a fraction
UPCAT Math Reviewer 7 to 8: SUM of all EVEN integers from 1 to 100? What part of x is yz?
Sum of natural numbers 1 to 100
How To Derive The Formula For The Sum of an Arithmetic Series
How To Find The Sum and Product of the Roots of a Quadratic Equation - Algebra
Fractions- Sum & Difference (Addition & Subtraction)
How to use the SUM function in Microsoft Excel
Find the Sum of Natural Numbers from 200 to 350 Inclusive
Learn how to determine the sum of a geometric finite series
Комментарии
 0:03:05
0:03:05
 0:01:04
0:01:04
 0:06:37
0:06:37
 0:19:50
0:19:50
 0:03:53
0:03:53
 0:03:10
0:03:10
 0:02:45
0:02:45
 0:00:19
0:00:19
 0:00:53
0:00:53
 0:03:20
0:03:20
 0:05:48
0:05:48
 0:09:06
0:09:06
 0:03:03
0:03:03
 0:03:46
0:03:46
 0:05:14
0:05:14
 0:01:55
0:01:55
 0:06:39
0:06:39
 0:02:26
0:02:26
 0:06:38
0:06:38
 0:10:43
0:10:43
 0:12:58
0:12:58
 0:00:38
0:00:38
 0:03:15
0:03:15
 0:02:42
0:02:42