filmov
tv
Simple Pendulum - Simple Harmonic Motion Derivation using Calculus

Показать описание
Content Times:
0:00 Simple Harmonic Motion Review
1:57 Simple Pendulum Definition
3:28 Pendulum Restoring Force
4:45 Net Tangential Force
5:47 Bringing in Arc Length
7:20 Small Angle Approximation
9:10 Solving for Angular Frequency
10:03 Solving for Period
10:32 Position, Velocity, and Acceleration
12:03 Angular Velocity and Angular Frequency in the same equation?
Next Video: Physical Pendulum - Period Derivation and Demonstration using Calculus
Previous Video: Simple Harmonic Motion Derivations using Calculus (Mass-Spring System)
#Derivation #SimpleHarmonicMotion #SimplePendulum
Simple Pendulum in Harmonic Motion
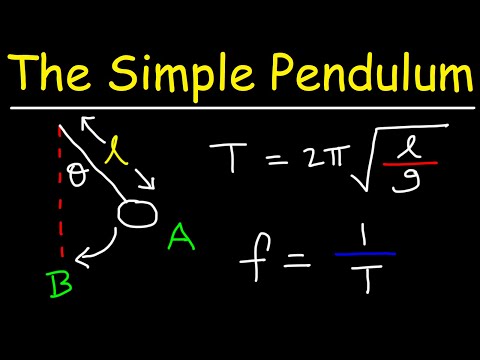
The Simple Pendulum
Simple Pendulum and SHM (Simple Harmonic Motion) | Class 11 | IIT JEE
1D10.50 Simple Harmonic Motion and Uniform Circular Motion
Simple Pendulum
An Overview of Simple Pendulum: Oscillation, Period and Frequency
Simple Harmonic Motion and Pendulum | Physics
Physics Review: Simple Harmonic Motion #14 The Simple Pendulum
The Cycloid Pendulum #physics #cycloid #pendulum
Simple Pendulum - Simple Harmonic Motion Derivation using Calculus
Simple Harmonic Motion: Hooke's Law
simple pendulum
Simple Harmonic Motion
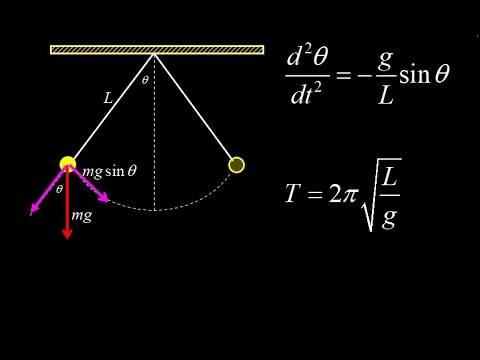
Derivation of simple pendulum period, equation of motion and example. Sine expansion for a pendulum.
Simple pendulum ! Class 11
Simple Pendulum
Period of a Pendulum | Simple harmonic motion and rotational motion | AP Physics 1 | Khan Academy
How do you derive the period of oscillation for a pendulum?
Simple Pendulum.#shorts ...
Pendulums | Oscillations and mechanical waves | Physics | Khan Academy
Simple Pendulum
Time period of a pendulum depends on its length | Oscillation| Physics
Simple Harmonic Motion: Crash Course Physics #16
Derive the expression for time period of oscillating Bob of simple pendulum
Комментарии
 0:08:21
0:08:21
 0:26:25
0:26:25
 0:09:35
0:09:35
 0:00:26
0:00:26
 0:04:24
0:04:24
 0:04:21
0:04:21
 0:07:40
0:07:40
 0:02:57
0:02:57
 0:01:00
0:01:00
 0:13:30
0:13:30
 0:04:49
0:04:49
 0:00:10
0:00:10
 0:00:25
0:00:25
 0:06:59
0:06:59
 0:00:15
0:00:15
 0:00:25
0:00:25
 0:09:25
0:09:25
 0:09:45
0:09:45
 0:00:06
0:00:06
 0:14:46
0:14:46
 0:01:08
0:01:08
 0:01:31
0:01:31
 0:09:11
0:09:11
 0:00:10
0:00:10