Simple Pendulum and SHM (Simple Harmonic Motion) | Class 11 | IIT JEE

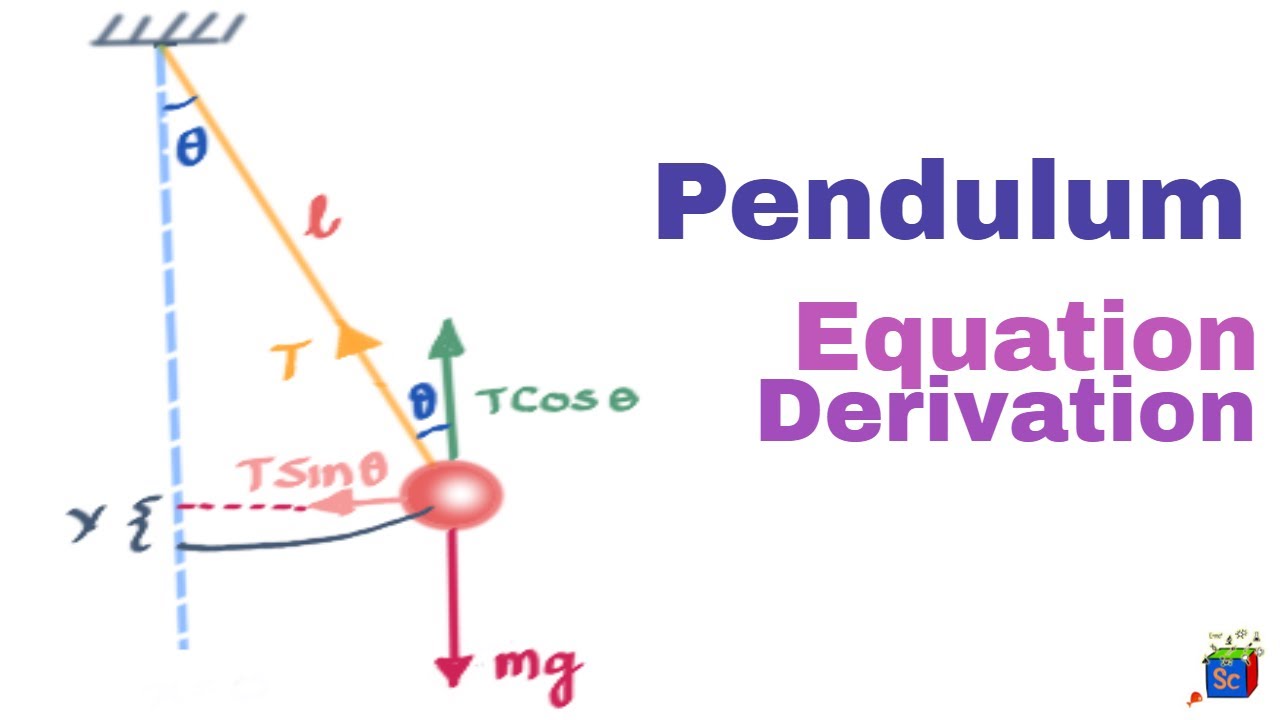
A pendulum is a mechanical system capable of doing SHM. It consists of a mass attached to a string or rod that is free to swing back and forth under the influence of gravity.

The swinging motion of a pendulum is an example of a simple harmonic motion (SHM), which is a type of periodic motion that follows a predictable pattern.

In a pendulum, the restoring force is the force of gravity acting on the mass. This force pulls the mass towards the equilibrium position, which is the position where the pendulum is in its lowest point. As the pendulum swings away from the equilibrium position, the restoring force increases and eventually causes the mass to change direction and swing back towards the equilibrium position. This swinging motion continues back and forth in a periodic pattern.

The equations that describe the motion of a pendulum in SHM are:

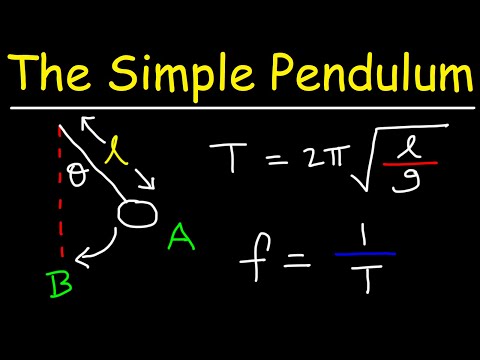
The period, T, of a pendulum is given by: T = 2π √(L/g)
The frequency, f, of a pendulum is given by: f = 1/T = 1/(2π √(L/g))
The angular displacement, θ, of a pendulum is given by: θ = θ0 * sin(ωt)
The angular velocity, ω, of a pendulum is given by: ω = dθ/dt = θ0 * ω * cos(ωt)
The angular acceleration, α, of a pendulum is given by: α = dω/dt = -θ0 * ω^2 * sin(ωt)
where L is the length of the pendulum, g is the acceleration due to gravity, θ0 is the maximum displacement of the pendulum from the equilibrium position, and ω is the angular frequency of the pendulum.

[TheScienceCube]

Covers:
📚 Study Guides & Tips for on how to excel in physics: For Class 11 and AP Physics students
🎓 Exclusive Content & Previews: Be the first to access new videos and materials.
📝 Common Mistakes & Things to Remember: Avoid pitfalls and learn the secrets to success.

[mahananda_maiti]

I have so many confusion about this small topic, now it is clear to me. Thank You sir.

[aymenzidane]

Thank you so much, you're the only one I found who explained why to put ay = 0.

[manazirahsan]

Bro.. Your mathmetical proof is very logical.. Thanks a lot bro

[Lily-tpui]

Thank you so much this was really clear xxx

[rodericksibelius]

When the swing is raised and released, it will move freely back and forth due to the force of gravity on it. The swing continues moving back and forth without any extra outside help until friction (between the air and the swing and between the chains and the attachment points) slows it down and eventually stops it. WHAT THEN IS THE FORMULA TO KNOW THE TIME WHEN IT PRACTICALLY STOPPED?

[dimlighty]

Why do you write 'm · a_y = T · cosθ - mg'?
Can't it be 'm · a_y = mg - T · cosθ' in the case when ball is moving down?

[sbti]

why you took Tcos theta = mg ?you could also take mgcos theta = T when we take components of mg.
which one is correct

[Harminder_Saini]

Thanks for explaining this so well. My professor made this overly complicated.

[spsi]

Thanks for posting the video. Question, how do you determine what the maximum force is of the mass on the string with an initial velocity (as if someone pushed the mass not just let it drop)?

[thephenomenals]

Sir can you tell about the energy in pendulum at a given instant

[son_charles]

I struggle with how you know where and when and how to use sin and tan and cos?
How do you know that Tcosø is used and TsinØ?

[AmitTiwari-izck]

Sir plse correct me
mgcos theta =T
Tcos theta = mg
Both can be done or not??
Plse answer asap

[trouble]

I don't understand really.. Y channel like urs is so underrated.

[madhujain]

But we use torque for angular shms how we r able to find time period by force analysis ???

[victormaxwellpeters]

Then ax is an x component of centripetal acceleration???
Even then for small change in angle partial should move in constant velocity and not accelerating, since velocity difference between point a to point b for small change in angle should be neglible

[caronlinemayson]

When you say that forces in y direction are approximately equal to zero because of angle, can’t you say that they are equal to zero because the body isn’t moving up or down?

[zayan]

Hi Sir, I Have Joined The WhatsApp Group. I Had Some Doubts For The Simple Pendulum, Could You Explain?

[mikaelafrias]

Hello, but do i still use the T equation if i have a given angle?

[kingzer]

Why was not mg resolved into its components??