filmov
tv
A math olympiad problem that looks complicated, but it's easy to solve
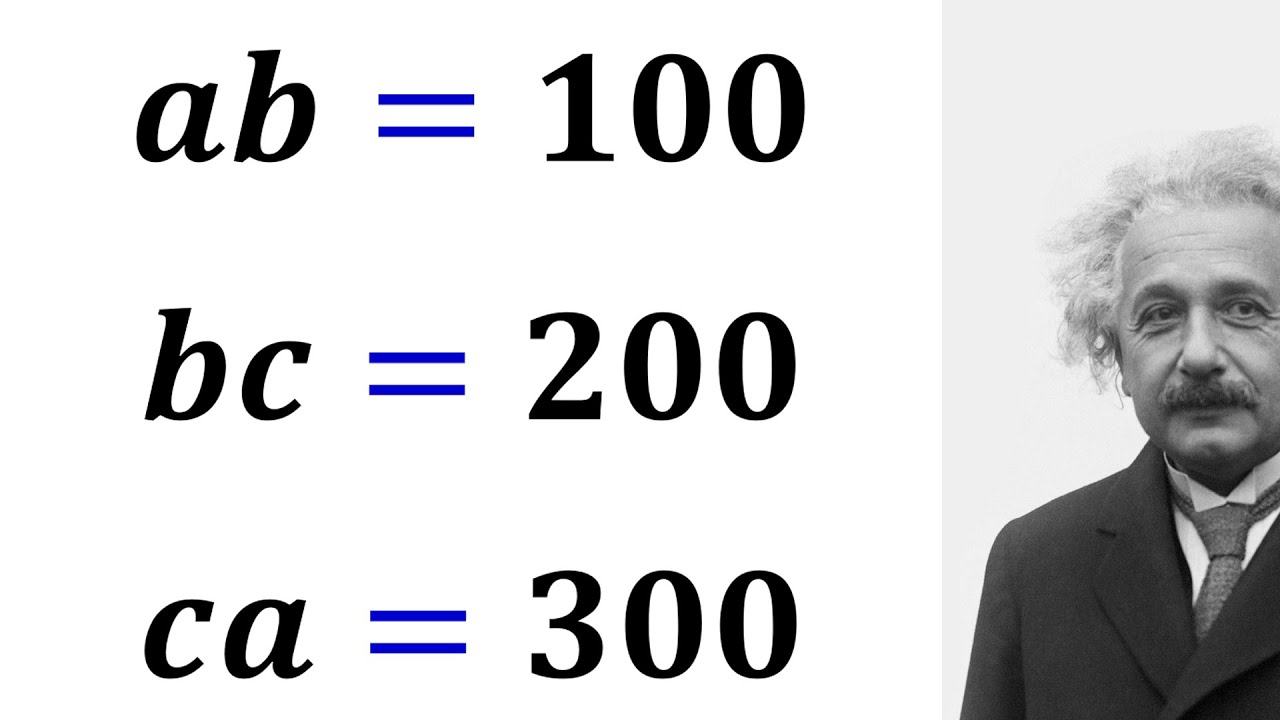
Показать описание
What do you think about this question? If you're reading this ❤️. Have a great day!
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
A beautiful international math olympiad problem
You, me, and my first International Math Olympiad problem
Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1
The unexpectedly hard windmill question (2011 IMO, Q2)
A math olympiad problem that looks complicated, but it's easy to solve
Solving the hardest question of a British Mathematical Olympiad
Norway Math Olympiad Question | You should be able to solve this!
Challenging Math Olympiad Problem | Geometry Question | Mathematics | 2 Methods
Math Olympiad | A Nice Algebra Problem | Find x and y
Regional Math Olympiad Problem
Mexico - A Nice Math Olympiad Exponential Problem
This U.S. Olympiad Coach Has a Unique Approach to Math
Germany - Math Olympiad Problem | Be Careful!
A Nice Math Olympiad Exponential Equation 3^x = X^9
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Iceland Math Olympiad Problem
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Luxembourg - Math Olympiad Question | You should know this trick
Japanese Math Olympiad Problem | A Nice Math Problem : Comparison
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988
Thailand | Math Olympiad Question | Nice Algebra Equation
Solving An Insanely Hard Problem For High School Students
Комментарии
 0:01:00
0:01:00
 0:31:21
0:31:21
 0:06:40
0:06:40
 0:16:03
0:16:03
 0:10:23
0:10:23
 0:11:26
0:11:26
 0:03:21
0:03:21
 0:25:44
0:25:44
 0:10:07
0:10:07
 0:13:55
0:13:55
 0:08:36
0:08:36
 0:03:20
0:03:20
 0:10:06
0:10:06
 0:02:34
0:02:34
 0:01:54
0:01:54
 0:02:54
0:02:54
 0:08:40
0:08:40
 0:10:49
0:10:49
 0:02:51
0:02:51
 0:04:15
0:04:15
 0:00:52
0:00:52
 0:08:03
0:08:03
 0:01:26
0:01:26
 0:07:27
0:07:27