filmov
tv
Concrete Mathematics, problem 3.31

Показать описание
Proving an inequality in two variables, involving the floor function. We draw contour plots, which make this problem almost obvious.
This nice problem was taken from 𝐶𝑜𝑛𝑐𝑟𝑒𝑡𝑒 𝑀𝑎𝑡ℎ𝑒𝑚𝑎𝑡𝑖𝑐𝑠 textbook — problem 31 from the 3rd chapter.
Source: Source: R. L. Graham, D. E. Knuth, O. Patashnik, 𝐶𝑜𝑛𝑐𝑟𝑒𝑡𝑒 𝑀𝑎𝑡ℎ𝑒𝑚𝑎𝑡𝑖𝑐𝑠. 𝐴 𝑓𝑜𝑢𝑛𝑑𝑎𝑡𝑖𝑜𝑛 𝑓𝑜𝑟 𝑐𝑜𝑚𝑝𝑢𝑡𝑒𝑟 𝑠𝑐𝑖𝑒𝑛𝑐𝑒 (2nd ed.), Addison-Wesley Professional, 1994.
This nice problem was taken from 𝐶𝑜𝑛𝑐𝑟𝑒𝑡𝑒 𝑀𝑎𝑡ℎ𝑒𝑚𝑎𝑡𝑖𝑐𝑠 textbook — problem 31 from the 3rd chapter.
Source: Source: R. L. Graham, D. E. Knuth, O. Patashnik, 𝐶𝑜𝑛𝑐𝑟𝑒𝑡𝑒 𝑀𝑎𝑡ℎ𝑒𝑚𝑎𝑡𝑖𝑐𝑠. 𝐴 𝑓𝑜𝑢𝑛𝑑𝑎𝑡𝑖𝑜𝑛 𝑓𝑜𝑟 𝑐𝑜𝑚𝑝𝑢𝑡𝑒𝑟 𝑠𝑐𝑖𝑒𝑛𝑐𝑒 (2nd ed.), Addison-Wesley Professional, 1994.
Concrete Mathematics, problem 3.31
Concrete Mathematics
Concrete Mathematics - ASMR in Nature
Concrete Mathematics, problem 2.31
21 September Hamster Kombat Daily Combo Card
Integer Word Problems (Concrete Situations)
Growing up Pentecostal... #short
Magic Math with fingers|Finger Maths|Abacus|Finger Abacus #math#mathematics#abacus#shorts
HSN | Today's Super-Special Gifts - Gifts for Her 11.16.2024 - 11 AM
2023 send and 6000 send bce present past animals🎁//🔥ppa// #animals #youtubeshorts #shorts
#simplification #tricks
How to divide fractions?
how to construct 30 degree angle using compass | 30° angle
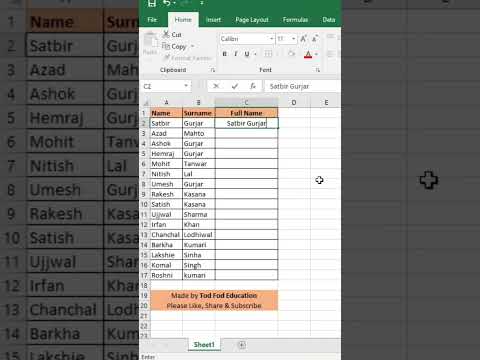
Flash Fill- Full Name- Excel tips & Tricks from @todfodeducation
How to convert meter to inch and feet ?#shots#calculator #inch #foot #meter
Toilet overflows and floods apartment in Ottawa #shorts
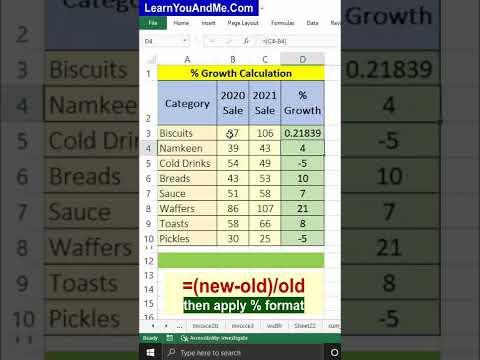
Calculate % increase or percent growth in Excel | Sale Growth percent in Excel | Percent increase
Describe your perfect vacation. #philippines #angelescity #expat #travel #filipina #phillipines
A case that shocked Canada in 2012😳 #shorts
SUM Formula in Excel | Add Total Values #shorts #excel
5 fingers + Gyroscope 🔥 #pubgm #pubgmobile #sevou #bgmi #levinho
Izzy Has To Stay 8 Hours After The Show Wraps
Number Patterns | MathHelp.com
Area and perimeter of square | Ayushi teacher | Area and perimeter #maths #area #perimeter
Комментарии
 0:08:56
0:08:56
 0:00:21
0:00:21
 0:00:55
0:00:55
 0:14:35
0:14:35
 0:00:14
0:00:14
 0:07:42
0:07:42
 0:00:15
0:00:15
 0:00:29
0:00:29
 1:00:00
1:00:00
 0:00:11
0:00:11
 0:00:11
0:00:11
 0:00:15
0:00:15
 0:00:13
0:00:13
 0:00:08
0:00:08
 0:00:43
0:00:43
 0:00:24
0:00:24
 0:01:00
0:01:00
 0:00:16
0:00:16
 0:00:14
0:00:14
 0:00:10
0:00:10
 0:00:29
0:00:29
 0:00:51
0:00:51
 0:01:01
0:01:01
 0:00:16
0:00:16