filmov
tv
how to construct 30 degree angle using compass | 30° angle

Показать описание
how to construct 30 degree angle using compass | 30° angle
30 degree angle construction with compass
#practicalgeometry
#class7maths
#maths
#geometry
#geometricconstruction
30 degree angle construction with compass
#practicalgeometry
#class7maths
#maths
#geometry
#geometricconstruction
constructing an angle of 30° degree || How to construct 30° degrees
how to construct 30 degree angle using compass | 30° angle
30 Degree Angle Construction Tutorial || 30 Degree Angle Construction || Compass Angle || Geometry
30 degree angle with compass | 30° Angle Construction
how to construct 30 degree angle with compass#shorts#viralshorts#yt shorts#RB knowledge explore
How to construct 30 degree angle with compass.....
30 degree angle construction / how to construct 30 degree angle using compass #shorts #viral #video
How to Construct 30 degree angle with compass | #shorts #short #ytshort #shortsvideo
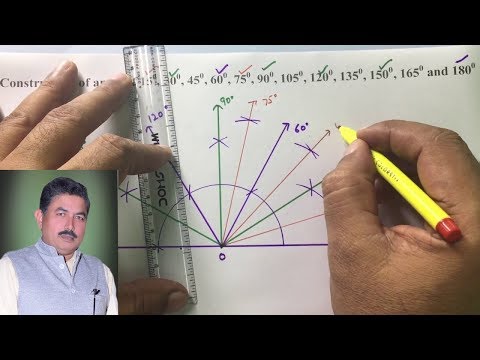
Construction of angle of 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165 and 180 degree new
How to construct 30 degree angle.
How to Construct 30, 45, 60, 90, and 120 degrees
How to construct a 30-degree angle
How to Construct a 30 Degree Angle? | Don't Memorise
Construct a 30 degree angle
how to construct 30 degree using compass. by #master maths#...
30 Degrees Angle Construction |How to Construct 30 Degree Angle|Constructing 30 Degree Angle #shorts
How to construct 30 degree angle using compass | 30° angle
30 degree angle construction | how to construct angles
How to Construct 30 degree in | Technical drawing | BASIC Technology
HOW TO CONSTRUCT ANGLE 30 DEGREE in | Technical drawing | Basic Technology
How to construct 30 degree angle using compass | 30 degree Angle | Geometry
How to Construct 30, 60, 90, and 120 Degree Angles
How to Construct 30, 60 and 120 Degree Angles in one go | Don't Memorise
How to construct 30 degree angle with compass 💥 30° angle #practicalgeometry #shorts #maths #viral...
Комментарии
 0:00:35
0:00:35
 0:00:13
0:00:13
 0:01:24
0:01:24
 0:00:15
0:00:15
 0:00:20
0:00:20
 0:01:45
0:01:45
 0:00:18
0:00:18
 0:00:10
0:00:10
 0:06:19
0:06:19
 0:02:08
0:02:08
 0:05:02
0:05:02
 0:01:41
0:01:41
 0:01:29
0:01:29
 0:01:22
0:01:22
 0:01:26
0:01:26
 0:00:14
0:00:14
 0:00:25
0:00:25
 0:01:00
0:01:00
 0:03:50
0:03:50
 0:01:00
0:01:00
 0:00:31
0:00:31
 0:03:36
0:03:36
 0:02:37
0:02:37
 0:00:14
0:00:14