filmov
tv
Domain, range, vertical & horizontal asymptotes, and removable discontinuity of a rational function
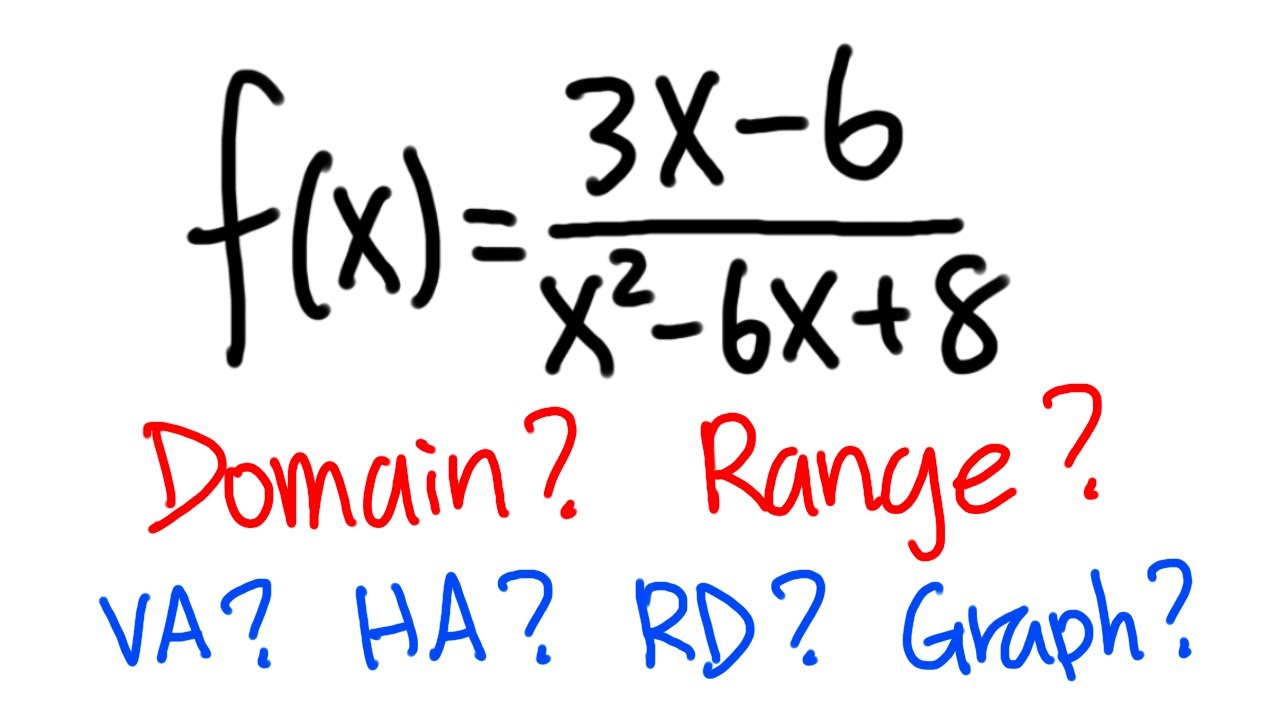
Показать описание
How to find the domain, range, removable discontinuity, vertical asymptote, and horizontal asymptote of a rational function. This is a must-know topic for both of your precalculus and calculus 1 classes. Subscribe to @bprpcalculusbasics for more calculus basics.
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
Rational Graphs Made Easy Find the vertical and horizontal asymptote
Find the vertical and horizontal asymptotes
Domain, range, vertical & horizontal asymptotes, and removable discontinuity of a rational funct...
Identifying vertical, horizontal asymptotes and holes
Vertical, Horizontal, Domain, Range restrictions, Shading
Dominate Domain, Range, & Slope of Horizontal & Vertical Lines
How to find vertical & horizontal asymptotes, domain, range, x, y-intercept of a rational functi...
Functions - Vertical Line Test, Ordered Pairs, Tables, Domain and Range
Identify Domain Vertical Horizontal Oblique Asymptotes xy Intercepts Holes. Rational Equations
How to determine, domain range, and the asymptote for an exponential graph
FINDING THE VERTICAL/HORIZONTAL ASYMPTOTE, AND DOMAIN/RANGE OF A FUNCTION | GEN MATH
Vertical Line Test
Graphing Rational Functions Using Transformations With Vertical and Horizontal Asymptotes
Identify Horizontal, Vertical Asymptotes, x and y Intercepts, Domain Range, Holes For Rational
Identify Points Of Discontinuities, Horizontal And Vertical Asymptotes. Domain Range. Part 1
How to find Domain, Range and Asymptotes (Horizontal & Vertical) of Rational Functions, Short Tr...
RATIONAL FUNCTIONS || DOMAIN, X-INTERCEPT, Y-INTERCEPT, VETICAL ASYMPTOTE AND HORIZONTAL ASYMPTOTE
Domain and Range of a Horizontal Line.
Rational Graph Vertical Asymptotes Horizontal Asymptote
Rational function (Domain, Range, horizontal & vertical asymptote, x and y intercept)
JMO MATH | Domain Range of Rational functions using horizontal asymptote and vertical asymptote.
Rational Function (Domain, Range, Vertical Asymptote and Horizontal Asymptote), Case 2- Gen. Math
How To Find The Vertical Asymptote of a Function
Evaluate the limits from a graph with horizontal and vertical asymptotes
Комментарии
 0:10:50
0:10:50
 0:03:54
0:03:54
 0:07:53
0:07:53
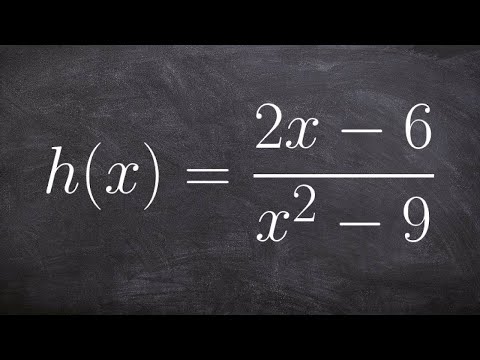 0:02:16
0:02:16
 0:02:46
0:02:46
 0:05:58
0:05:58
 0:14:44
0:14:44
 0:10:54
0:10:54
 0:04:45
0:04:45
 0:08:30
0:08:30
 0:04:22
0:04:22
 0:05:27
0:05:27
 0:18:30
0:18:30
 0:08:24
0:08:24
 0:07:31
0:07:31
 0:09:00
0:09:00
 0:11:52
0:11:52
 0:03:55
0:03:55
 0:07:15
0:07:15
 0:06:00
0:06:00
 0:06:20
0:06:20
 0:21:03
0:21:03
 0:10:54
0:10:54
 0:02:42
0:02:42