filmov
tv
33. Neural Nets and the Learning Function
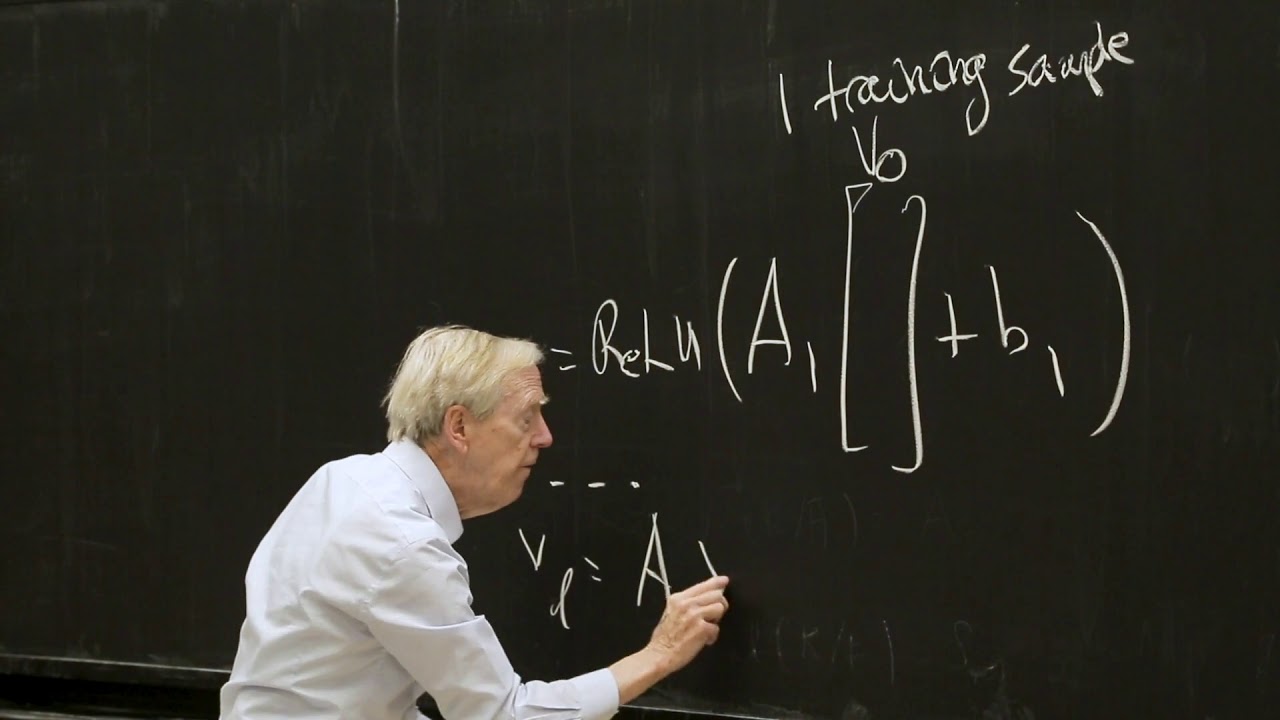
Показать описание
MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018
Instructor: Gilbert Strang
This lecture focuses on the construction of the learning function F, which is optimized by stochastic gradient descent and applied to the training data to minimize the loss. Professor Strang also begins his review of distance matrices.
License: Creative Commons BY-NC-SA
Instructor: Gilbert Strang
This lecture focuses on the construction of the learning function F, which is optimized by stochastic gradient descent and applied to the training data to minimize the loss. Professor Strang also begins his review of distance matrices.
License: Creative Commons BY-NC-SA
33. Neural Nets and the Learning Function
Neural Network In 5 Minutes | What Is A Neural Network? | How Neural Networks Work | Simplilearn
Neural Networks Explained in 5 minutes
But what is a neural network? | Chapter 1, Deep learning
ANN vs CNN vs RNN | Difference Between ANN CNN and RNN | Types of Neural Networks Explained
What is Recurrent Neural Network (RNN)? Deep Learning Tutorial 33 (Tensorflow, Keras & Python)
Equivariant Neural Networks | Part 1/3 - Introduction
Neural Network Architectures & Deep Learning
Graph Neural Networks - a perspective from the ground up
The Neural Network, A Visual Introduction
Dendrites: Why Biological Neurons Are Deep Neural Networks
Neural Networks and Deep Learning: Crash Course AI #3
The Complete Mathematics of Neural Networks and Deep Learning
Neural Networks Pt. 2: Backpropagation Main Ideas
1. Introduction to Artificial Neural Network | How ANN Works | Soft Computing | Machine Learning
Why Transformer over Recurrent Neural Networks
Gradient descent, how neural networks learn | Chapter 2, Deep learning
The Convolutional Neural Network (Animated Introduction)
Neural Networks - Introduction to the Maths Behind
T33.2: A Neural Network Model of Continual Learning with Cognitive Control
Physics Informed Neural Networks (PINNs) [Physics Informed Machine Learning]
MAMBA from Scratch: Neural Nets Better and Faster than Transformers
NeuralNet Package - Neural Networks for Business Analytics with R (Rstudio) 25/33
Recurrent Neural Networks | RNN LSTM Tutorial | Why use RNN | On Whiteboard | Compare ANN, CNN, RNN
Комментарии
 0:56:07
0:56:07
 0:05:45
0:05:45
 0:04:32
0:04:32
 0:18:40
0:18:40
 0:05:39
0:05:39
 0:16:00
0:16:00
 0:18:51
0:18:51
 0:09:09
0:09:09
 0:14:28
0:14:28
 0:13:52
0:13:52
 0:25:28
0:25:28
 0:12:23
0:12:23
 5:00:53
5:00:53
 0:17:34
0:17:34
 0:08:09
0:08:09
 0:01:00
0:01:00
 0:20:33
0:20:33
 0:09:04
0:09:04
 0:11:15
0:11:15
 0:19:36
0:19:36
 0:34:32
0:34:32
 0:31:51
0:31:51
 0:02:30
0:02:30
 0:22:21
0:22:21