filmov
tv
36 factors, again!
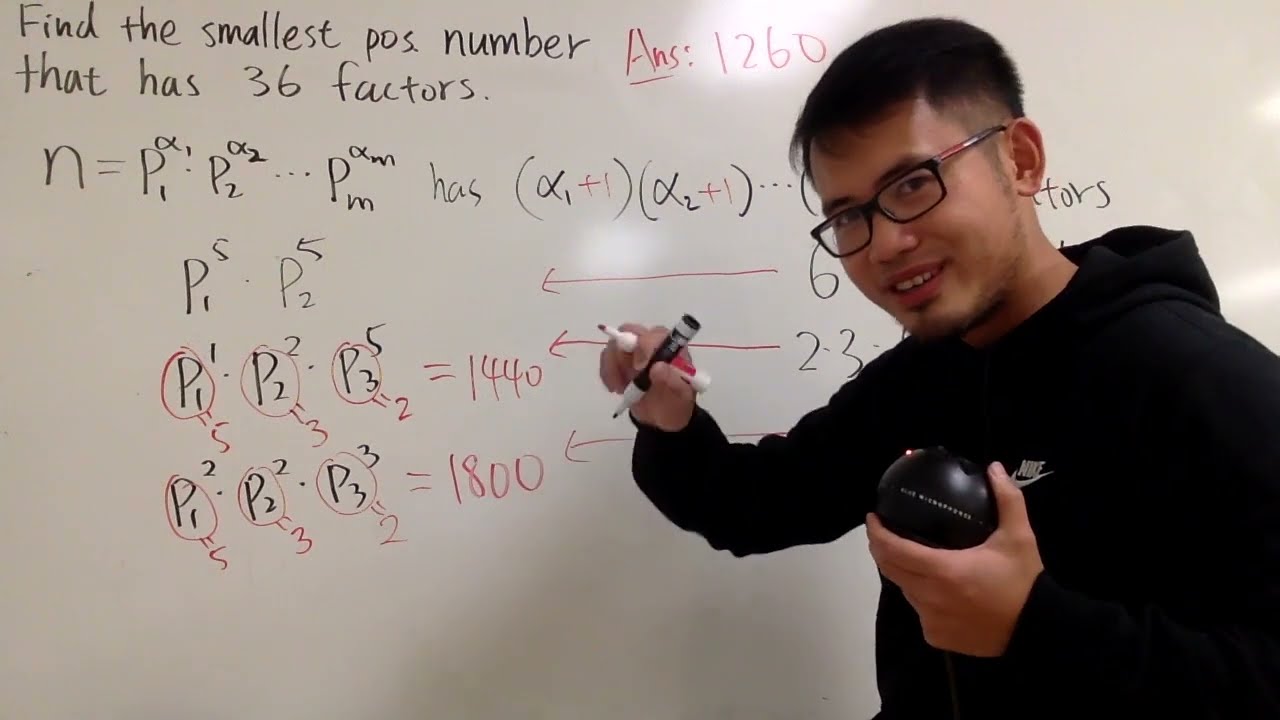
Показать описание
Special thanks to my number 1 supporter, *ChiaChia*, and her two star cats, Oreo and Luna.
Find the smallest whole number that has 36 factors,
fun number theory problem,
how to find the number of divisors,
how to find the number of factors,
blackpenredpen,
math for fun,
36 factors, again!
Greatest Common Factor | How to Find the Greatest Common Factor (GCF)
KAWĘ pij tylko o TEJ porze. Tak działa na jelita, mózg, wątrobę
How To Factor Polynomials The Easy Way!
Doubles Addition Facts Song
2-Digit by 2-Digit Multiplication | Math with Mr. J
AI Is Rewriting the Rules of Work: Futurist Ian Beacraft Explains Why Jobs are Dead
СУХОЕ ГОЛОДАНИЕ 36 ЧАСОВ ✨ | ОТВЕТЫ НА ВАЖНЫЕ ВОПРОСЫ | Мой опыт голодания...
How to Find a Fraction of a Whole Number | Fractions of Whole Numbers
Multiplying Whole Numbers and Fractions | Math with Mr. J
Improper Fractions to Mixed Numbers | How to Convert | Math with Mr. J
How to Simplify a Mixed Number | Math with Mr. J
3-Digit by 2-Digit Multiplication | Math with Mr. J
Dividing 3-Digit Numbers by 2-Digit Numbers | Math with Mr. J
How to know if it’s time to change careers | The Way We Work, a TED series
America Stole This Plane and Turned It Into a Monster
Best Advice to Small Business Owners
China's Exports To Vietnam Skyrocket Ahead of Xi's Visit | Insight with Haslinda Amin 4/14...
Simplifying Ratios Explained | How to Simplify a Ratio | Math with Mr. J
Memory Loss and Concentrating Issues
Olivia sings 'Roar' by Katy Perry | The Voice Stage #36
Volatility here to stay? Key Market Factors Going Forward Explained!
Multiply a Whole Number by a Decimal | Math with Mr. J
Multiply a Decimal by a Decimal | Math with Mr. J
Комментарии
 0:10:19
0:10:19
 0:07:39
0:07:39
 0:16:00
0:16:00
 0:11:54
0:11:54
 0:01:56
0:01:56
 0:04:54
0:04:54
 1:07:10
1:07:10
 0:10:10
0:10:10
 0:06:12
0:06:12
 0:06:14
0:06:14
 0:05:54
0:05:54
 0:05:15
0:05:15
 0:05:03
0:05:03
 0:07:02
0:07:02
 0:04:29
0:04:29
 0:23:27
0:23:27
 0:03:26
0:03:26
 0:48:10
0:48:10
 0:06:51
0:06:51
 0:01:56
0:01:56
 0:07:52
0:07:52
 0:15:53
0:15:53
 0:04:06
0:04:06
 0:03:56
0:03:56