filmov
tv
Multivariable calculus, class # 24: change of variables
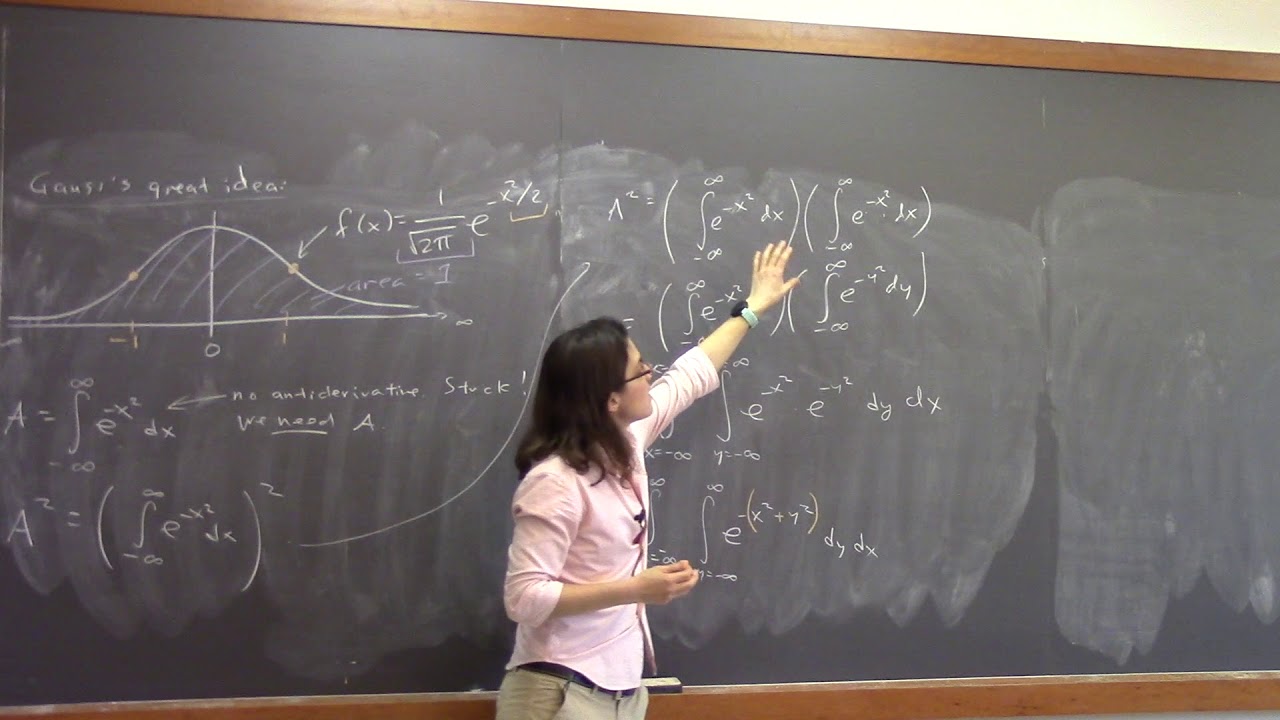
Показать описание
Mathematician spotlight: Colin Adams
We briefly discuss knot invariants and the petal number. We show the amazing trick to compute the area under the bell curve (Gaussian distribution) by squaring the area and turning it into a double integral, then converting to polar coordinates. We give the formula for the Jacobian area factor for a (u,v) substitution in general, then show that it is a generalization of u-substitutions from single-variable calculus. We do two examples of (u,v) substitution, a linear one (where we can solve for x and y in terms of u and v) and a nonlinear one (where we use the inverse of the determinant of the inverse transformation matrix).
We briefly discuss knot invariants and the petal number. We show the amazing trick to compute the area under the bell curve (Gaussian distribution) by squaring the area and turning it into a double integral, then converting to polar coordinates. We give the formula for the Jacobian area factor for a (u,v) substitution in general, then show that it is a generalization of u-substitutions from single-variable calculus. We do two examples of (u,v) substitution, a linear one (where we can solve for x and y in terms of u and v) and a nonlinear one (where we use the inverse of the determinant of the inverse transformation matrix).
Multivariable calculus, class # 24: change of variables
Multivariable Calc Class #24, Part 1, Chain Rule for Paths, Gradient Vectors, and Polar Coordinates
Multivariable Calc., Class #24, Pt 2, Chain Rule for Paths, Gradient Vectors, and Polar Coordinates
ALL of calculus 3 in 8 minutes.
How to Make it Through Calculus (Neil deGrasse Tyson)
What is the Hardest Calculus Course?
Vector Calculus Complete Animated Course for DUMMIES
Multivariable Calculus Final Exam Review
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
Vector Calculus-Class-24-Vector Integration basic problems
Partial Derivatives - Multivariable Calculus
Double and triple integrals | Lecture 24 | Vector Calculus for Engineers
Worldwide Multivariable Calculus Section 1.1 #24
Multivariable Calculus | Finding a limit with polar coordinates.
Calculus 3 Full Course | Calculus 3 complete course
Describing Surfaces Explicitly, Implicitly & Parametrically // Vector Calculus
What Is The 'Normal Vector?' - Calculus 3
24: Divergence - Valuable Vector Calculus
Flow Integrals and Circulation // Big Idea, Formula & Examples // Vector Calculus
Worldwide Multivariable Calculus Ch2.8 #24
Vector Calculus 24: The Principal Normal and Curvature of a Planar Curve
Geometric Meaning of the Gradient Vector
Multivariable Calculus ch1.4 #23
Multivariable Calculus | A special double integral.
Комментарии
 0:49:08
0:49:08
 0:33:26
0:33:26
 0:11:12
0:11:12
 0:08:10
0:08:10
 0:03:38
0:03:38
 0:01:44
0:01:44
 0:46:44
0:46:44
 1:17:35
1:17:35
 0:11:24
0:11:24
 0:26:08
0:26:08
 1:00:33
1:00:33
 0:09:26
0:09:26
 0:02:03
0:02:03
 0:03:04
0:03:04
 8:19:22
8:19:22
 0:11:05
0:11:05
 0:00:59
0:00:59
 0:11:01
0:11:01
 0:08:43
0:08:43
 0:06:49
0:06:49
 0:16:24
0:16:24
 0:14:51
0:14:51
 0:01:32
0:01:32
 0:03:57
0:03:57