filmov
tv
The way math should be taught

Показать описание
Second channel: @tibees2
Book link is an Amazon affiliate link.
Editing by Noor Hanania
The way math should be taught
Grant Sanderson (3Blue1Brown): Best Way to Learn Math | AI Podcast Clips
Anyone Can Be a Math Person Once They Know the Best Learning Techniques | Po-Shen Loh | Big Think
Math isn't hard, it's a language | Randy Palisoc | TEDxManhattanBeach
A Genius Mathematician Suggested This Simple Idea — And It Could Transform The Way You Do Math
Stop Trying to Understand Math, Do THIS Instead
Five Principles of Extraordinary Math Teaching | Dan Finkel | TEDxRainier
100-Year-Old Math Teacher Slams The 'Common Core' Method
Powers and Exponents Rules – Algebra Rules to Simplify Expressions with Powers and Exponents
How To Self-Study Math
60-Second Strategy: Math Partners
Math Classrooms Should Be Places of Surprise and Wonder | Matthew Oldridge | TEDxChathamKent
How to Get Better at Math
How to Understand Math Intuitively?
The Beauty of Math - Zimmer [Motivational]
This Video Will Make You Better At Math
This simple game makes kids better at math
The Simplest Math Problem No One Can Solve - Collatz Conjecture
How to become a Math Genius.✔️ How do genius people See a math problem! by mathOgenius
Is math discovered or invented? - Jeff Dekofsky
Can Math Help Repair Democracy? | Sam Wang | TED
Math Foundations – Basic Math Skills every Adult should know
Learn Math With Zero Knowledge
What happened to 'new math'?
Комментарии
 0:14:47
0:14:47
 0:03:22
0:03:22
 0:03:53
0:03:53
 0:08:55
0:08:55
 0:08:49
0:08:49
 0:05:21
0:05:21
 0:14:42
0:14:42
 0:02:09
0:02:09
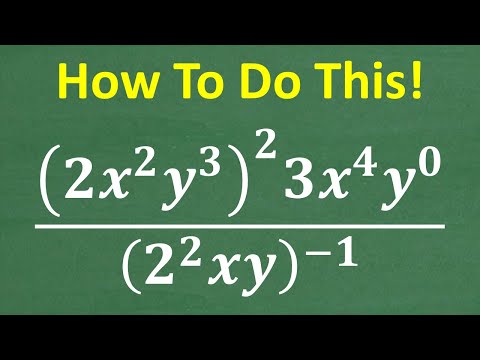 0:13:51
0:13:51
 0:08:16
0:08:16
 0:01:06
0:01:06
 0:18:00
0:18:00
 0:09:41
0:09:41
 0:08:28
0:08:28
 0:06:38
0:06:38
 0:04:52
0:04:52
 0:02:07
0:02:07
 0:22:09
0:22:09
 0:15:24
0:15:24
 0:05:11
0:05:11
 0:12:05
0:12:05
 0:10:41
0:10:41
 0:09:48
0:09:48
 0:35:37
0:35:37