filmov
tv
Powers and Exponents Rules – Algebra Rules to Simplify Expressions with Powers and Exponents

Показать описание
Help with Middle and High School Math
Test Prep for High School Math, College Math, Teacher Certification Math and More!
Popular Math Courses:
Math Foundations
Math Skills Rebuilder Course:
Pre-Algebra
Algebra
Geometry
Algebra 2
Pre-Calculus
• MIDDLE & HIGH SCHOOL MATH
• HOMESCHOOL MATH
• COLLEGE MATH
• TEST PREP MATH
• TEACHER CERTIFICATION TEST MATH
Algebra Basics: Laws Of Exponents - Math Antics
Power of a Power | Exponent Rules | Math with Mr. J
Exponent Rules with Examples
Simplifying Exponents With Fractions, Variables, Negative Exponents, Multiplication & Division, ...
Exponent Rules: The Power to Power Rule!
Laws of exponents #ajmathematicaltutor
Rules of Exponents (Multiplying, Dividing, Roots) Algebra with JusticeTheTutor #math #shorts
13 - Exponent Rules of Algebra (Laws of Exponents, How to Multiply & Add Exponents)
How to Solve Logarithms Equations/Find the value of X?
Introduction to Exponents
What is an Exponent? | An Intro to Exponents | Math with Mr. J
Algebra Basics: Exponents In Algebra - Math Antics
Power Rule of Exponents - Cool math
LAWS OF EXPONENT | Mathematics Animation
Simplifying Exponents | Expressions & Equations | Grade 8
Exponents and the Laws of Exponents (Powers)
Exponent Rules: Laws and Examples
Exponent: power of 10 #exponents #powerof10 #power #algebra #mathtricks #mathstricks #shorts
The Maths Prof: The Rules of Indices / Exponents (part 1)
Laws of Exponents - Basics in Simplifying Expressions
Exponent Rules: Product to a Power Explained!
Power of a Power Rule (Exponents)
Exponent Formulas #maths #exponents
LAWS OF EXPONENTS | MATHS TRICKS
Комментарии
 0:13:46
0:13:46
 0:04:11
0:04:11
 0:06:53
0:06:53
 0:11:48
0:11:48
 0:03:43
0:03:43
 0:00:10
0:00:10
 0:00:15
0:00:15
 0:25:57
0:25:57
 0:06:04
0:06:04
 0:10:33
0:10:33
 0:07:21
0:07:21
 0:12:14
0:12:14
 0:13:14
0:13:14
 0:08:55
0:08:55
 0:05:05
0:05:05
 0:08:46
0:08:46
 0:00:07
0:00:07
 0:00:15
0:00:15
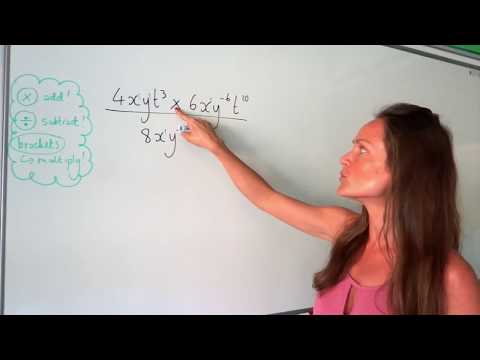 0:10:18
0:10:18
 0:17:54
0:17:54
 0:05:07
0:05:07
 0:09:25
0:09:25
 0:00:08
0:00:08
 0:00:42
0:00:42