filmov
tv
Probability & Statistics (17 of 62) The 'At Least One or Once' Rule

Показать описание
In this video I will explain the “at least one or once rule”.
Next video in series:
Probability & Statistics (17 of 62) The 'At Least One or Once' Rule
Statistics: Ch 5 Discrete Random Variable (17 of 27) The Binomial Probability Distribution
Statistics: Ch 6 The Normal Probability Distribution (17 of 28) Find Area Between 2 x-Values: Ex. 1
Randomness: Crash Course Statistics #17
Math 14 5.2.17-T Find the probability of fewer than 3
Statistics: Ch 4 Probability in Statistics (17 of 74) Chi-Squared Test of Goodness Fit: Ex. 2 + TAPI
Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams
Probability of sample proportions example | Sampling distributions | AP Statistics | Khan Academy
Joint, Marginal and Conditional distributions (Week-1)
Math 14 4.4.17 Find the probability of winning the jackpot.
MINI LECTURE 17: Maximum Ignorance Probability (a bit more technical)
Ex: Determine a Probability with AND using a Table
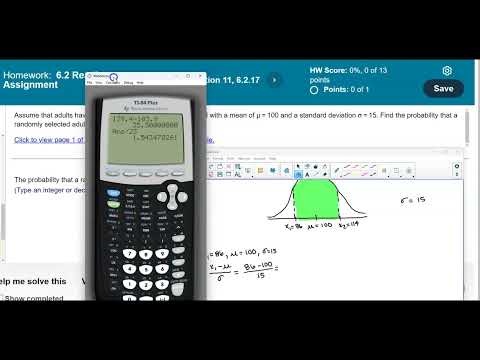
Math 14 6.2.17 Find the probability that a randomly selected adult has an IQ between 86 and 114.
Addition rule for probability | Probability and Statistics | Khan Academy
Physics 32.5 Statistical Thermodynamics (17 of 39) Microstates & Probability of a 100-Coin Toss
Ex: Basic Example of Finding Probability From a Table
Probability Theory 17 | Standard Deviation
Probability Top 10 Must Knows (ultimate study guide)
Probability of Consecutive Coin Flips
Lec-17: Discrete And Continuous Random Variable | Probability and Statistics
Relative complement or difference between sets | Probability and Statistics | Khan Academy
Probability Part 1: Rules and Patterns: Crash Course Statistics #13
Probability - Drawing Venn Diagrams
Probability of Normal distribution simple and good example(PART-1)
Комментарии
 0:02:00
0:02:00
 0:05:56
0:05:56
 0:05:00
0:05:00
 0:12:07
0:12:07
 0:06:01
0:06:01
 0:03:17
0:03:17
 0:16:59
0:16:59
 0:07:35
0:07:35
 2:05:15
2:05:15
 0:05:11
0:05:11
 0:05:03
0:05:03
 0:02:06
0:02:06
 0:05:52
0:05:52
 0:10:43
0:10:43
 0:07:53
0:07:53
 0:02:40
0:02:40
 0:08:38
0:08:38
 0:50:51
0:50:51
 0:00:25
0:00:25
 0:18:54
0:18:54
 0:06:15
0:06:15
 0:12:01
0:12:01
 0:06:13
0:06:13
 0:08:47
0:08:47