filmov
tv
Probability of Consecutive Coin Flips
Показать описание
Probability of Consecutive Coin Flips
Consecutive Coin Flips - Numberphile
Coin flipping probability | Probability and Statistics | Khan Academy
The coin flip conundrum - Po-Shen Loh
Quant Interview Puzzle: Expected Tosses for 3 Consecutive Heads - Recurrence & Markov Chains
Scientists Just Proved Coin Tosses Are Flawed Using 350,757 Coin Flips
Coin Tosses needed for Consecutive Heads | Quant Interview Questions
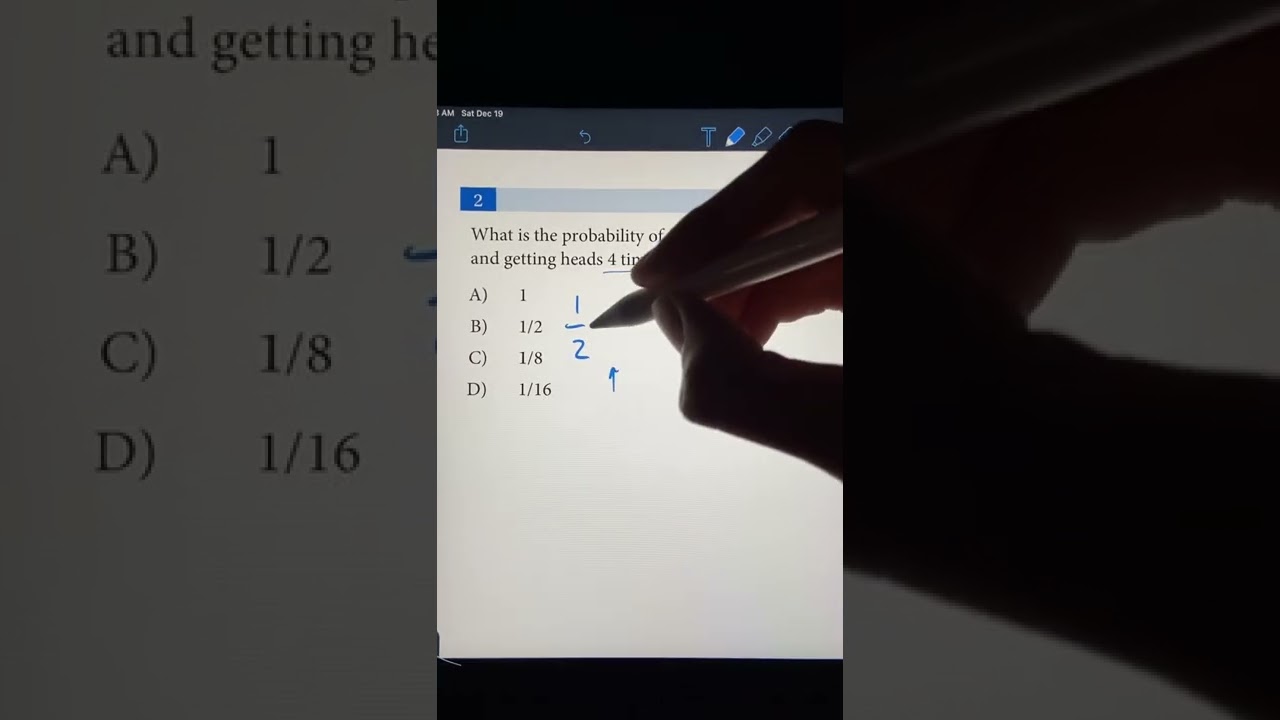
Probability of consecutive coin flips #probability #coinflip #shorts
Probability: consecutive coin flips #probability #coinflip #shorts
Exactly three heads in five flips | Probability and Statistics | Khan Academy
Counter-Intuitive Probability. Coin Flips To HH Versus HT Are Not The Same!
probability of consecutive coin flips | probability trees #probability #probabilitytricks #shorts
Expected Coin Flips for k Heads in a Row
Probability of Exactly 5 Heads in 8 Coins Flip
Neil deGrasse Tyson's Coin Flip Experiment 🧐
Probability test | coin flips #probability #coinflip #shorts
Flipping 10 heads in a row: Full video
Why Coin Flips are NOT 50/50
A coin is tossed (m+n) times,Probability of getting exactly m consecutive heads.
2022 China Math Olympiad: Probability of Coin Flips (fill-in-the-blank problem)
Probability tricks for tossing of coins| #shorts #probability #cupidtwinversion #mathtricks
33 - Most Consecutive Coin Flips
What is the probability of flipping heads 3 times in a row?
Expected Rolls for N Consecutive Sixes and Tosses for N Consecutive Heads
Комментарии
 0:00:25
0:00:25
 0:08:06
0:08:06
 0:09:20
0:09:20
 0:04:23
0:04:23
 0:22:28
0:22:28
 0:04:39
0:04:39
 0:05:26
0:05:26
 0:00:05
0:00:05
 0:00:06
0:00:06
 0:06:51
0:06:51
 0:10:20
0:10:20
 0:00:18
0:00:18
 0:07:20
0:07:20
 0:04:31
0:04:31
 0:00:47
0:00:47
 0:00:05
0:00:05
 0:04:59
0:04:59
 0:01:49
0:01:49
 0:07:15
0:07:15
 0:00:59
0:00:59
 0:00:14
0:00:14
 0:00:24
0:00:24
 0:04:12
0:04:12
 0:07:09
0:07:09