Find the speed of a particle on a spiral trajectory given the position vector (2D kinematics)

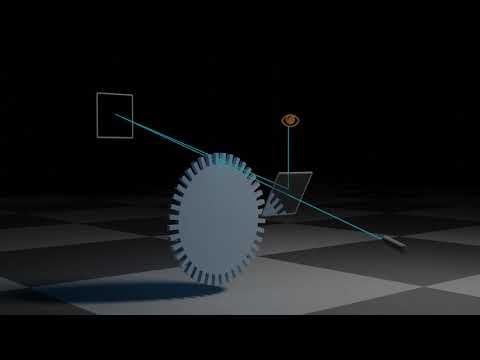
Given the position vector for a particle on a spiral path r(t)=0.1tcos(pi/2t)i-hat+0.1tsin(pi/2t)j-hat, we find the speed of the particle at t=1s.

We begin with an animation of the particle on a spiral trajectory and discuss how the position vector is creating a spiral here: the angular velocity of the particle is constant and the radius is increasing.

We view a second animation with the velocity vector for the particle included, and we see that the speed is increasing with time: this is because the angular velocity stays the same as the radius increases, meaning the particle has more distance to cover for each time increment.

To compute the speed of a particle on a spiral trajectory, we need to take the time derivative of the position vector to obtain the velocity vector. This requires both the product rule and chain rule. Finally, we compute the magnitude of the velocity vector by using the Pythagorean theorem, and we're done!