filmov
tv
An Exponential System
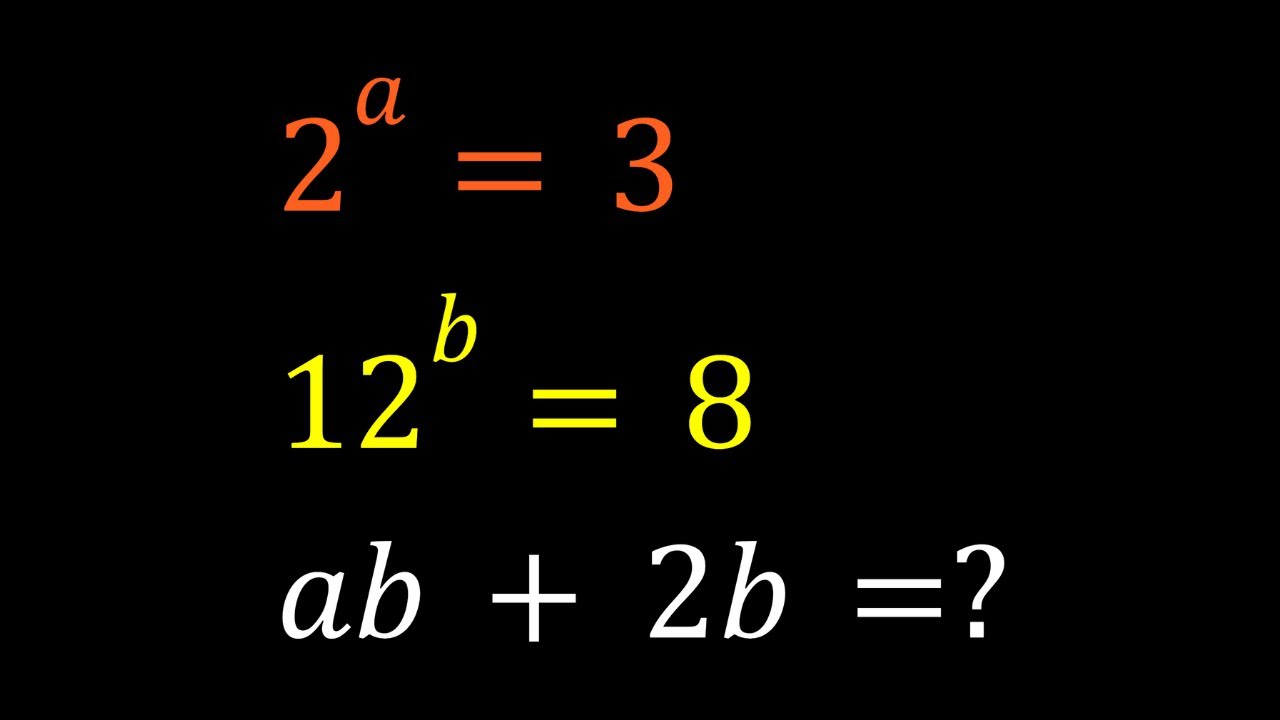
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ExponentialEquations
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
An Exponential System
An Exponential System
An Exponential System | Real Solutions
An Exponential System with Parameters
Solving An Exponential System
Working with an Exponential System
Solving an Exponential System in Two Ways
Solving an Exponential System in Two Ways
Maths Olympiad Problem | An Exponential Equation
Solving An Exponential System | Algebra
I Solved An Exponential System
Solving an Exponential System with Logarithms
A Nice Exponential System | Two Ways
Solving an exponential system of equations
Math Olympiad | How to Solve the System of Exponential Equations?
A Quick and Easy Exponential System
Solving Exponential Equation
A Homemade Exponential System
Solving A Nice Exponential System
An Exponential System
Solving A Nice And Easy Exponential System
A Nice Exponential System
How to Graph Exponential Functions
A Non-Standard Exponential System
Комментарии
 0:08:24
0:08:24
 0:06:48
0:06:48
 0:10:11
0:10:11
 0:06:38
0:06:38
 0:00:53
0:00:53
 0:08:36
0:08:36
 0:09:44
0:09:44
 0:10:59
0:10:59
 0:03:06
0:03:06
 0:00:44
0:00:44
 0:08:22
0:08:22
 0:10:36
0:10:36
 0:09:26
0:09:26
 0:08:09
0:08:09
 0:03:59
0:03:59
 0:10:35
0:10:35
 0:00:56
0:00:56
 0:05:11
0:05:11
 0:09:00
0:09:00
 0:00:53
0:00:53
 0:09:38
0:09:38
 0:08:07
0:08:07
 0:00:40
0:00:40
 0:09:59
0:09:59