Henry Adams (3/12/21): Vietoris-Rips thickenings: Problems for birds and frogs

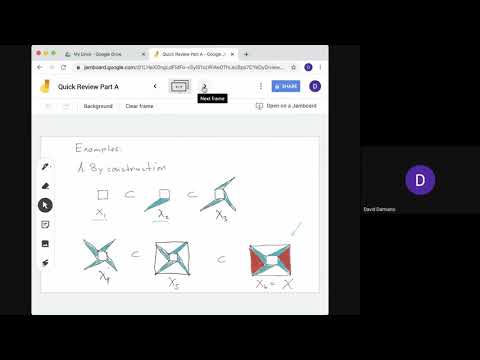
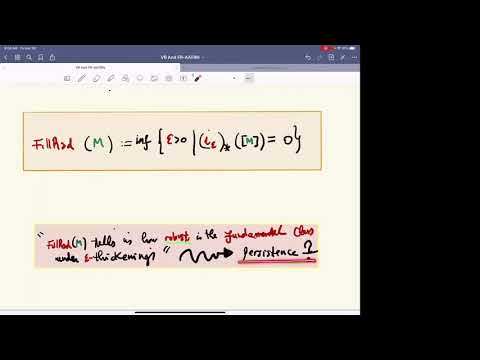
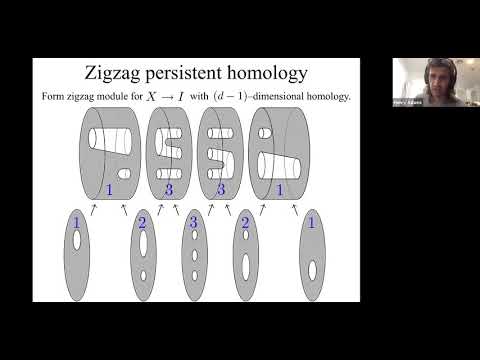
An artificial distinction is to describe some mathematicians as birds, who from their high vantage point connect disparate areas of mathematics through broad theories, and other mathematicians as frogs, who dig deep into particular problems to solve them one at a time. Neither type of mathematician thrives without the help of the other! In this talk, I will survey open problems related to Vietoris-Rips complexes that are attractive to both birds and frogs. Though Vietoris-Rips complexes are frequently used to approximate the shape of a dataset, many questions remain about their mathematical properties. Frogs may delight in open problems such as the homotopy types of Vietoris-Rips complexes of spheres, ellipsoids, tori, graphs, Cayley graphs of groups, geodesic spaces, subsets of the plane, and even the integer lattice Z^n with the taxicab metric for n at least 4. Birds may enjoy emerging connections between Vietoris-Rips complexes and a variety of areas in pure mathematics, including metric geometry (Gromov-Hausdorff distances), quantitative topology (Gromov's filling radius), measure theory (optimal transport), topological combinatorics (Borsuk-Ulam theorems), geometric group theory (finiteness properties of groups), and geometric topology (thick-thin decompositions).