Graphing a Parabolic Cylinder in 3D

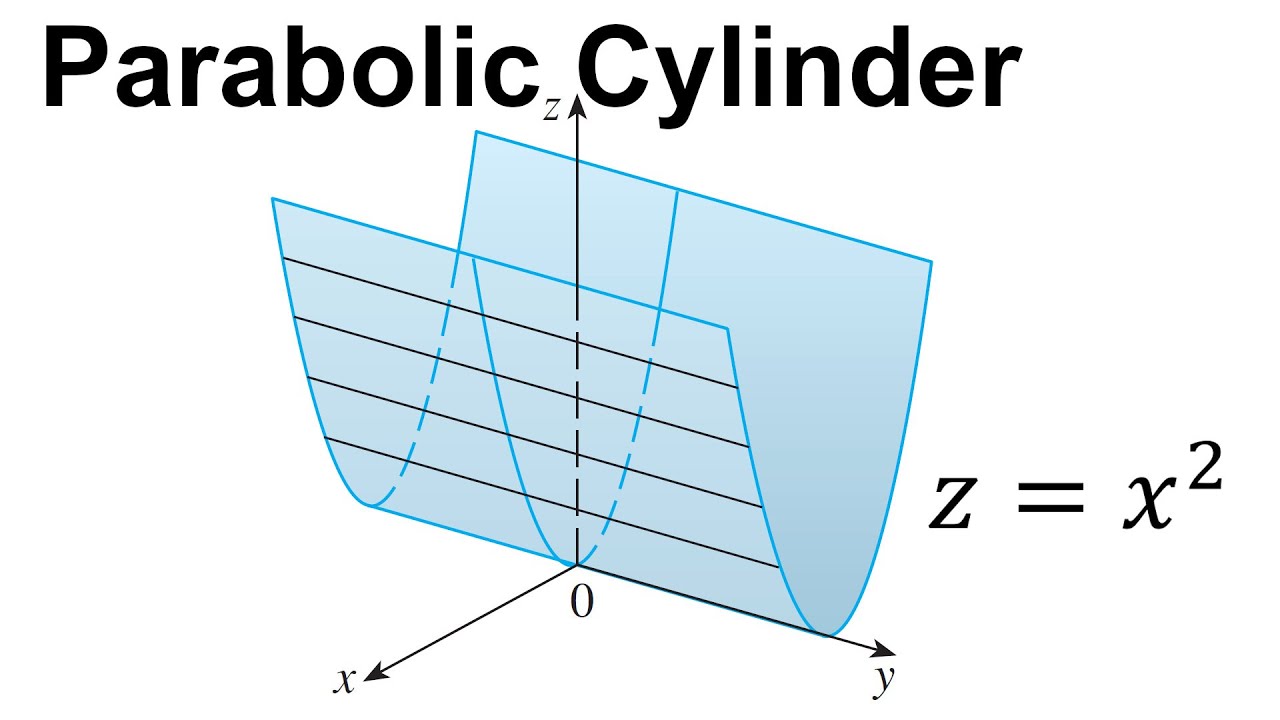
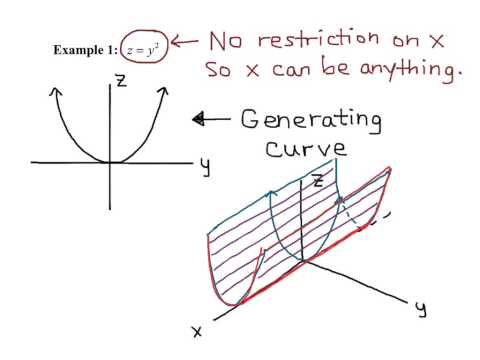
In this video I introduce cylinders and quadric surfaces and then do an example graphing out a parabolic cylinder. I first recap on the equation of a plane and equation of a sphere in 3D. A cylinder is defined as a 3D surface that consists of all lines (called rulings) that are parallel to a given line and pass through a given plane. I illustrate this by sketching the graph of the parabolic cylinder z = x^2. Since the y-variable is missing, this means that the parabola on the xz-plane can be extended along the y-axis to infinity. Note that the 2D parabolas are called traces, which are curves of intersection of the surfaces with planes parallel to the coordinate planes. Traces make it easier to sketch the surface, and in some cases are necessary to do so.

Time stamps:

- Recap on Planes and Spheres: 0:00
- Graphing cylinders and quadric surfaces using traces: 1:25
- Cylinders: 1:47
- Example 1: Parabolic Cylinder 2:05
- Cylinder has a missing variable in the equation: 6:31

Full video below:

------------------------------------------------------