filmov
tv
Deriving The Euler Equation
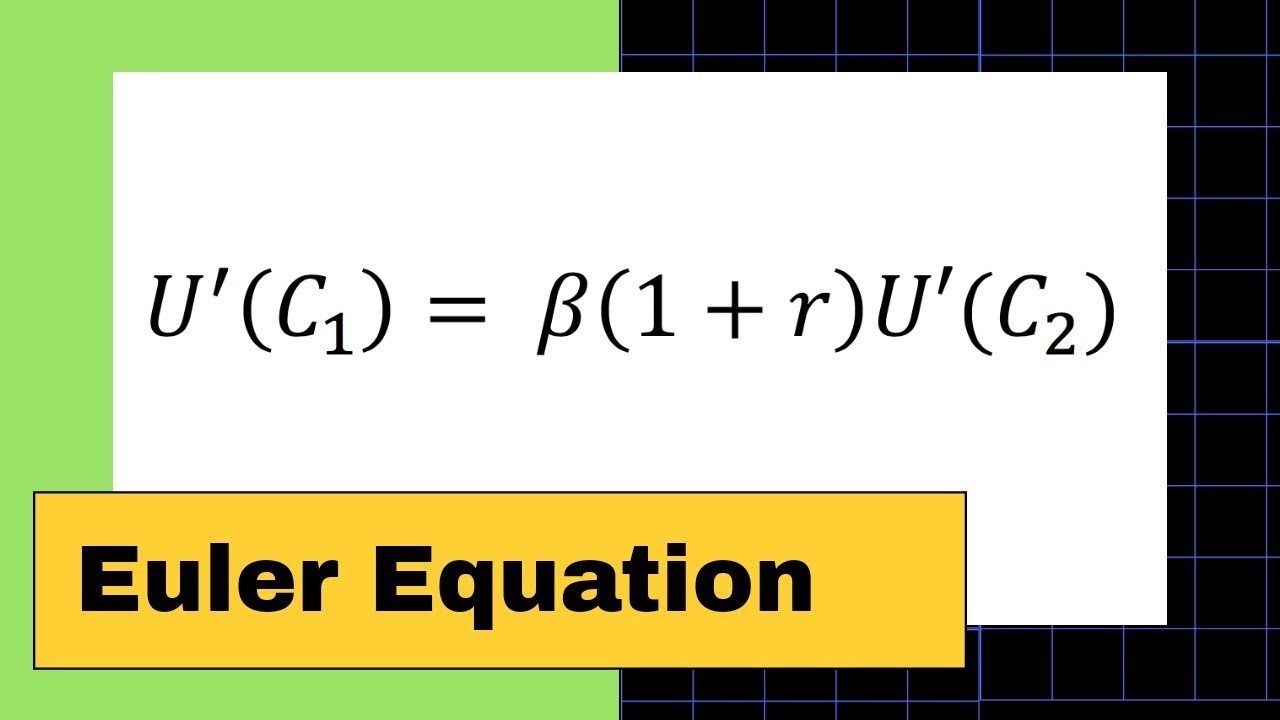
Показать описание
I algebraically derive the Euler equation in our intertemporal choice model and give some intuition as to what this means. We show graphically how this relates to the marginal rate of substitution and the interest rate.
We derive the Euler equation by assuming additively separable utility functions with a discount factor beta. The utility functions are strictly concave.
View the playlist to see how we build to this in previous videos. I derive the intertemporal budget constraint for a two-period model of intertemporal choice. I shall derive this for more periods. Check out the playlist for intertemporal macroeconomics as a whole, linked at the end of this video.
We discuss the assumptions of the two-period model of intertemporal choice. This involves consumers living for 2 periods. They can consume, save or borrow in these time periods, allowing for consumption that differs from their income in that period. In order to defer income to other periods, they can buy or sell one-period bonds with interest r.
We can then mathematically write the budget constraint for each of these periods. With a bit of substitution and rearranging, this gives us the intertemporal budget constraint. This says that the present value of consumption is equal to the present value of income. The consumer can thus not spend more than she earns, but will spend all of her income since more consumption is always assumed to increase her utility.
In future videos we shall look at borrowers and savers in more detail, examining what happens with a change in the interest rate, changes in income and other exogenous changes. In this one, we focus on how to find the Euler equation.
Subscribe for more videos looking at games of chance, tutorials, and everything to do with the industry. Put suggestions for video ideas in the comments section below and any feedback offered would be greatly appreciated.
We derive the Euler equation by assuming additively separable utility functions with a discount factor beta. The utility functions are strictly concave.
View the playlist to see how we build to this in previous videos. I derive the intertemporal budget constraint for a two-period model of intertemporal choice. I shall derive this for more periods. Check out the playlist for intertemporal macroeconomics as a whole, linked at the end of this video.
We discuss the assumptions of the two-period model of intertemporal choice. This involves consumers living for 2 periods. They can consume, save or borrow in these time periods, allowing for consumption that differs from their income in that period. In order to defer income to other periods, they can buy or sell one-period bonds with interest r.
We can then mathematically write the budget constraint for each of these periods. With a bit of substitution and rearranging, this gives us the intertemporal budget constraint. This says that the present value of consumption is equal to the present value of income. The consumer can thus not spend more than she earns, but will spend all of her income since more consumption is always assumed to increase her utility.
In future videos we shall look at borrowers and savers in more detail, examining what happens with a change in the interest rate, changes in income and other exogenous changes. In this one, we focus on how to find the Euler equation.
Subscribe for more videos looking at games of chance, tutorials, and everything to do with the industry. Put suggestions for video ideas in the comments section below and any feedback offered would be greatly appreciated.
Комментарии
 0:26:07
0:26:07
 0:13:40
0:13:40
 0:09:45
0:09:45
 0:07:25
0:07:25
 0:03:57
0:03:57
 0:04:08
0:04:08
 0:26:57
0:26:57
 0:08:42
0:08:42
 0:00:16
0:00:16
 0:09:27
0:09:27
 0:10:08
0:10:08
 0:07:50
0:07:50
 0:25:23
0:25:23
 0:06:56
0:06:56
 0:03:29
0:03:29
 0:06:03
0:06:03
 0:05:51
0:05:51
 0:11:10
0:11:10
 0:21:10
0:21:10
 0:14:45
0:14:45
 0:06:06
0:06:06
 0:41:28
0:41:28
 0:13:39
0:13:39
 0:11:16
0:11:16