filmov
tv
Drawing an Involute Spur Gear (HD)
Показать описание
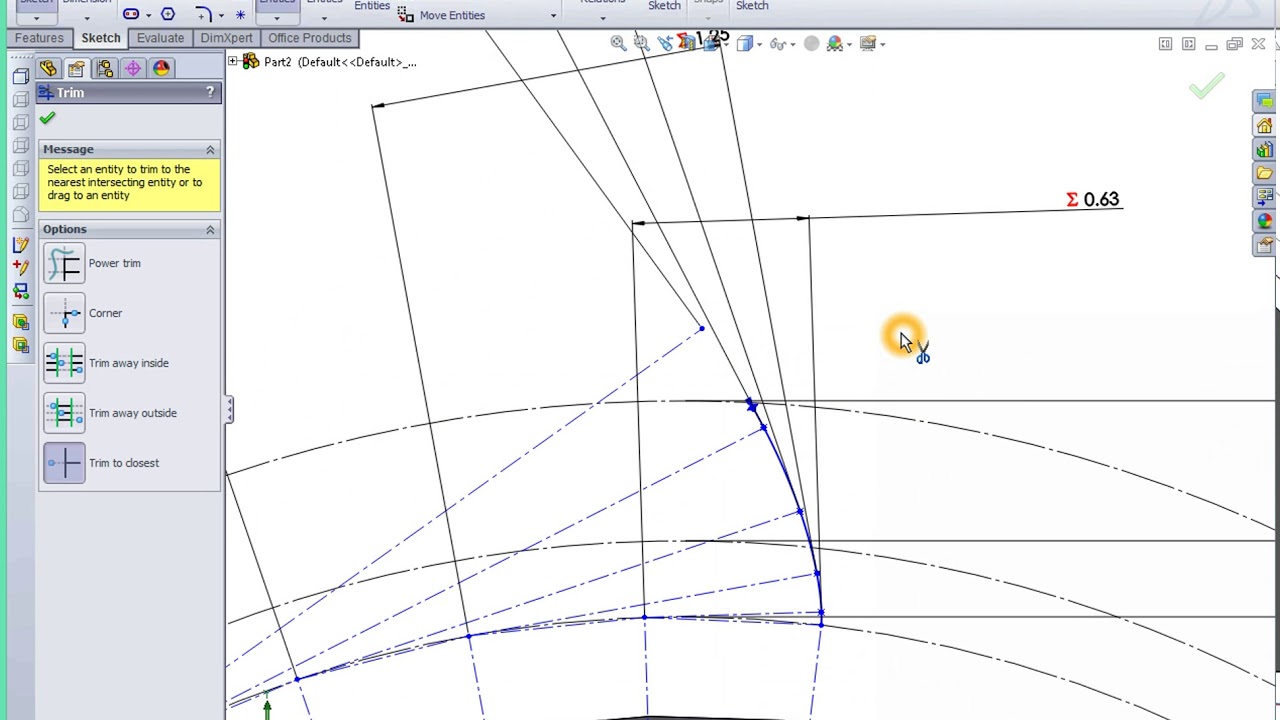
This video details the process of drawing an involute spur gear by hand in SolidWorks.
Drawing an Involute Spur Gear (HD)
Spur Gear Design 2 - Involute of the circle
Drawing an Involute Spur Gear from Scratch in Fusion 360
Creo Parametric - Spur Gear Design | Involute Curve
How To Draw An Involute Gear Tooth Profile| Machine Drawing | Edusquad
How to Draw Involute Gear Tooth Profile
Involute Gears Explained
Understand and Design Involute Spur Gears From Scratch |JOKO ENGINEERING|
INVOLUTE SPUR GEAR CONSTRUCTION, formulas and calculation involve, UNWIN'S
Mechanical Drawing 202 Ep. 1 - Introduction To Involute Spur Gears
How to draw a spur gear involute profile in AutoCAD/GStarCAD/ZwCAD with LitioLAB
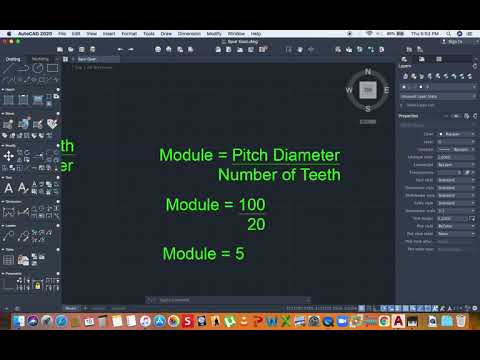
How to create spur gear in AUTOCAD (Approximate)
Drawing Gears with a Compass (simplified method)
How to make involute spur gear profile in solid works / Solid works tutorial Spur Gears part 1
Construction Of A Gear Tooth With Involute Curves
Spur Gears -part1(making spur gear of an involute curve)
How to design involute profile for a gear in AutoCAD
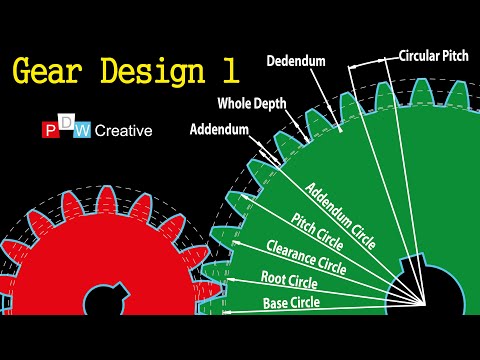
Spur Gear Design 1 - How gears work
Mechanical Drawing 202 Ep 3. Designing An Involute Spur Gear (Part 2)
INVOLUTE SPUR GEAR CONSTRUCTION part 1 | engineering drawing
Gear Design - Spur Gear (1) CATIA v5 r21 (involute curve Development)
Mechanical Drawing 202 Ep. 2 - Designing An Involute Spur Gear (Part 1)
AutoCAD 2D: Involute Profile of Spur Gear | TechTutorials
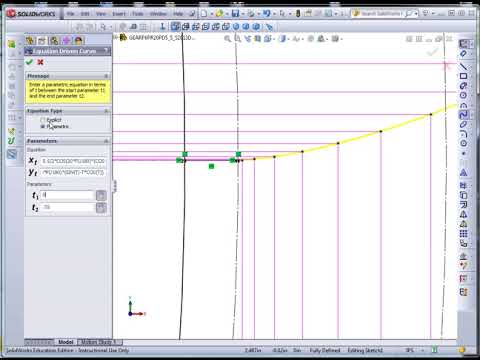
Equation Driven Involute Spur Gear in SolidWorks Part I
Комментарии
 0:24:01
0:24:01
 0:03:04
0:03:04
 0:18:03
0:18:03
 0:18:14
0:18:14
 0:19:39
0:19:39
 0:04:32
0:04:32
 0:06:40
0:06:40
 0:22:26
0:22:26
 0:32:37
0:32:37
 0:27:11
0:27:11
 0:01:28
0:01:28
 0:07:27
0:07:27
 0:03:02
0:03:02
 0:19:44
0:19:44
 0:01:11
0:01:11
 0:39:28
0:39:28
 0:04:00
0:04:00
 0:05:52
0:05:52
 0:29:49
0:29:49
 0:26:31
0:26:31
 0:12:41
0:12:41
 0:41:38
0:41:38
 0:06:28
0:06:28
 0:04:54
0:04:54