filmov
tv
You can add scalars and vectors! From Zero to Geo 1.11

Показать описание
In this video, I show that contrary to popular belief, you can add scalars and vectors! While this particular idea isn't terribly useful, with a bit of generalization it can lead the way to many useful things, such as multivectors.
Sorry for how long this video took to make! While the final product isn't that long, I rewrote parts of it so many times. I even removed a significant section at the last moment because it was too confusing. I hope that in the end, it was worth it and that this video is informative.
Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
p11
Richard Penner
Rosario
trb
Sections:
00:00 Introduction
00:39 Questions
01:14 Analogy with basis vectors
02:16 Exercise
02:48 Paravectors as a linear space
03:12 Zeros
03:58 General direct sums
05:10 Properties of direct sums
06:11 Conclusion
06:40 Rigorous Construction
Sorry for how long this video took to make! While the final product isn't that long, I rewrote parts of it so many times. I even removed a significant section at the last moment because it was too confusing. I hope that in the end, it was worth it and that this video is informative.
Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
p11
Richard Penner
Rosario
trb
Sections:
00:00 Introduction
00:39 Questions
01:14 Analogy with basis vectors
02:16 Exercise
02:48 Paravectors as a linear space
03:12 Zeros
03:58 General direct sums
05:10 Properties of direct sums
06:11 Conclusion
06:40 Rigorous Construction
You can add scalars and vectors! From Zero to Geo 1.11
Scalars & Vectors 2 : Adding Scalars
Scalars and Vectors
GCSE Physics - Scalar and Vector Quantities
Scalars, Vectors, and Vector Operations
“Adding” Scalars and Bivectors: Ridiculous?! A video for high-school teachers of Geometric Algebra...
“Adding” Scalars and Bivectors: Ridiculous?! A video for high-school teachers of Geometric Algebra...
Scalars, Vectors, Matrices, Tensors, etc explained | Linear Algebra Basics for Machine Learning
Span and System of Linear Equations (Week 2 & 3)
Can you add three unit vectors to get a unit vector?Does your answer change| H C verma solutions|
Scalars & Vectors 3 : Adding Vectors (Basic)
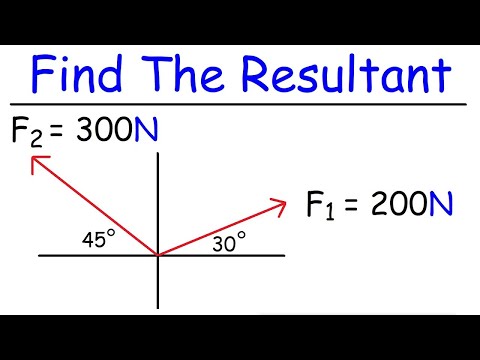
How To Find The Resultant of Two Vectors
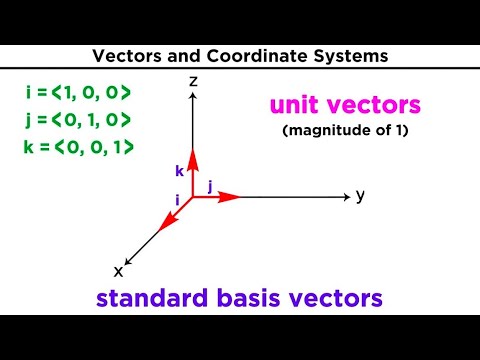
Introduction to Vectors and Their Operations
MCV4U - Find Magnitude of Vectors Multiplied by Scalars and Added
Everything You Need to Know About VECTORS
What is a vector?
Vector ADDITION of Multiple Vectors in 2 STEPS | Vector Physics | Class 11 Physics
Scalar/Vector quantities ✨#physics #study #elearn #shortsvideo
Why Can’t You Add a Vector to a Scalar?
Class 9 - Physics - Chapter 2 - Lecture 2 - 2.3 Scalars and Vectors - Allied Schools
adding and subtracting vectors #math #add #vector #shorts
How to Add Vectors? #maths #calculus #vector #matrix
Tip to tail Vector Addition
Adding Vectors - Triangle and Parallelogram Method
Комментарии
 0:09:00
0:09:00
 0:04:00
0:04:00
 0:11:21
0:11:21
 0:03:10
0:03:10
 0:10:42
0:10:42
 0:19:13
0:19:13
 0:19:13
0:19:13
 0:09:44
0:09:44
 1:53:51
1:53:51
 0:01:43
0:01:43
 0:06:24
0:06:24
 0:11:10
0:11:10
 0:10:17
0:10:17
 0:07:23
0:07:23
 0:17:42
0:17:42
 0:00:26
0:00:26
 0:00:23
0:00:23
 0:00:05
0:00:05
 0:00:24
0:00:24
 0:11:13
0:11:13
 0:00:19
0:00:19
 0:00:33
0:00:33
 0:00:32
0:00:32
 0:00:13
0:00:13