filmov
tv
How many ways can you join regular pentagons?

Показать описание
Thanks to Jane Street for supporting this video.
Curved-Crease Sculptures by Erik Demaine and Martin Demaine
Cookie. Clicker. Like that video is going to happen.
CORRECTIONS
- None yet, let me know if you spot anything!
Filming and editing by Alex Genn-Bash
Written and performed by Matt Parker
Produced by Nicole Jacobus
Music by Howard Carter
Design by Simon Wright and Adam Robinson
MATT PARKER: Stand-up Mathematician
Curved-Crease Sculptures by Erik Demaine and Martin Demaine
Cookie. Clicker. Like that video is going to happen.
CORRECTIONS
- None yet, let me know if you spot anything!
Filming and editing by Alex Genn-Bash
Written and performed by Matt Parker
Produced by Nicole Jacobus
Music by Howard Carter
Design by Simon Wright and Adam Robinson
MATT PARKER: Stand-up Mathematician
How many ways can you arrange a deck of cards? - Yannay Khaikin
How many ways can you join regular pentagons?
How many ways can you die in Minecraft?
How many ways can circles overlap? - Numberphile
I Can Show Numbers In So Many Ways | Math Song for Kids | How to Represent Numbers | Jack Hartmann
In how many ways can you select a committee of 3 out of 10 students
How many ways can you say '0'?
In How Many Different Ways Can You Kill Mario?
Beans ! for how many ways can Beans be used
How many ways can you join this roblox game? - Trailer
How many ways can letters be arranged
How to get: Method Three (How many ways can you join this roblox game?)
How Many Ways can you Arrange 5 Things? (Fundamental Counting Principle) (Permutations)
How Many Ways Can You Answer All The Questions of a 20 Question True-False Test?
How many ways can you say 'Love You'? | The Chopra Center - Deepak Chopra
How to get: Method SIx (How many ways can you join this roblox game?)
How Many Ways Can I Die In Peaceful Minecraft?
Sociocultural Linguistics | How many ways can you say I love you?
In how many ways can the letters of the word 'CALCUTTA' be arranged? | Viral Math Solution
how to get method 14 in how many ways can you join this roblox game?
how to get method 7 in how many ways can you join this roblox game!
COMBINATIONS with REPETITION - DISCRETE MATHEMATICS
How many ways can 12 students get into groups of 4?
Permutations, Combinations & Probability (14 Word Problems)
Комментарии
 0:03:42
0:03:42
 0:24:02
0:24:02
 0:22:25
0:22:25
 0:09:46
0:09:46
 0:03:44
0:03:44
 0:03:17
0:03:17
 0:03:10
0:03:10
 0:09:58
0:09:58
 0:00:49
0:00:49
 0:00:43
0:00:43
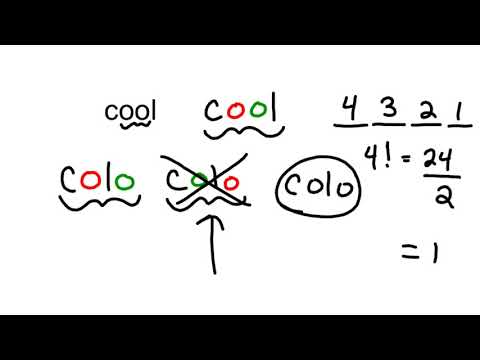 0:12:52
0:12:52
 0:00:08
0:00:08
 0:04:07
0:04:07
 0:01:20
0:01:20
 0:03:36
0:03:36
 0:00:17
0:00:17
 0:38:26
0:38:26
 0:02:15
0:02:15
 0:01:01
0:01:01
 0:01:01
0:01:01
 0:03:47
0:03:47
 0:13:35
0:13:35
 0:05:16
0:05:16
 0:21:17
0:21:17