filmov
tv
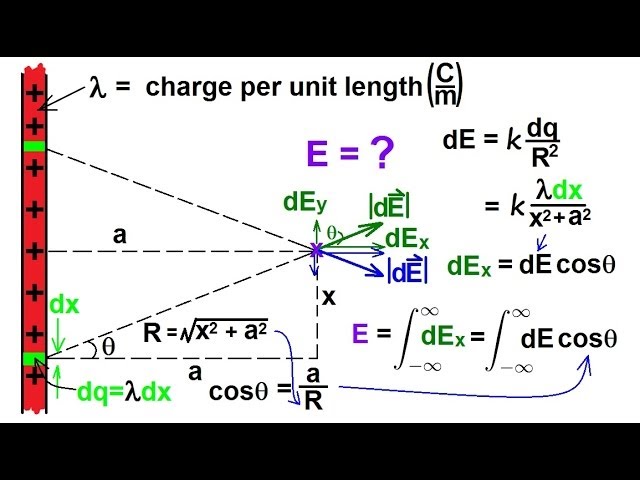
Physics 36 Electric Field (6 of 18) Infinite Line Charge
Показать описание
In this video I will find the electric field of an infinite line charge.
Physics 36 Electric Field (6 of 18) Infinite Line Charge
Physics 36 The Electric Field (5 of 18) The Electric Dipole
Physics 36 The Electric Field (8 of 18) Ring of Charge
Physics 37 Gauss's Law (6 of 16) Sphere With Uniform Charge
Physics 36 Electric Field (16 of 18) Finite Line Charge with Varying Linear Charge
Physics - E&M: Ch 36.1 The Electric Field Understood (6 of 17) Drawing Electric Field Lines Ex. ...
Physics 36 Electric Field (15 of 18) The Electric Dipole
Physics 36 The Electric Field (1 of 18)
Class 12 Physics Magnetism & Matter | Torque & P.E of a Magnetic Dipole | 12th Physics Numer...
Physics 36 Electric Field (18 of 18) Line Charge with Positive and Negative Charges
Physics 36 The Electric Field (9 of 18) Disc of Charge
Physics 36 The Electric Field (2 of 18)
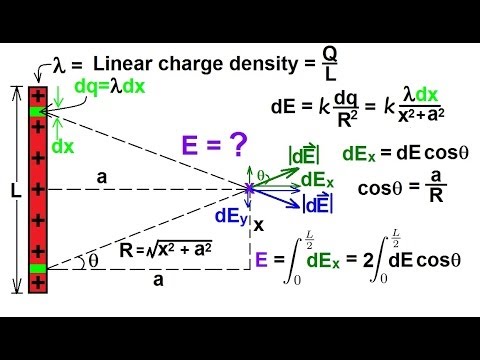
Physics 36 The Electric Field (7 of 18) Finite Length Line Charge
Electric Field Due To Point Charges - Physics Problems
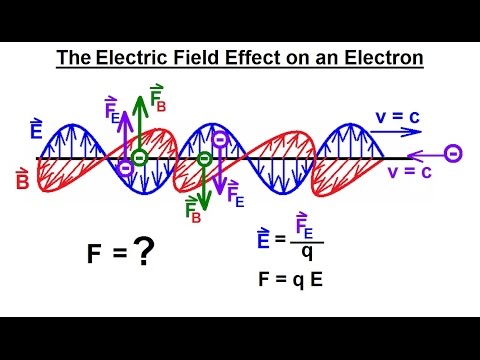
Particle Physics (36 of 41) What is a Photon? 20. The Electric Field
Physics - E&M: Ch 36.1 The Electric Field Understood (9 of 17) Find the Electric Field Ex. 1
Magnitude of electric field created by a charge | Physics | Khan Academy
Electric Fields: Crash Course Physics #26
Physics - E&M: Ch 36.1 The Electric Field Understood (10 of 17) Find the Electric Field Ex. 2
Physics 36 Electric Field (11 of 18) An Arc of Charge
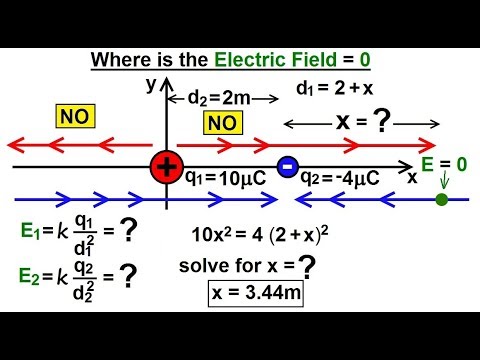
Physics - E&M: Ch 36.1 The Electric Field Understood (14 of 17) Find Where Electric Field=0
Physics 36 Electric Field (10 of 18) Horizontal Line Charge
Physics 36 Electric Field (14 of 18) Infinite Sheet of Charge: Method 2: Cartesian Coordinates
Electric Charge and Electric Fields
Комментарии
 0:11:32
0:11:32
 0:09:01
0:09:01
 0:11:41
0:11:41
 0:06:31
0:06:31
 0:10:53
0:10:53
 0:02:05
0:02:05
 0:13:20
0:13:20
 0:08:06
0:08:06
 0:59:02
0:59:02
 0:12:39
0:12:39
 0:08:14
0:08:14
 0:07:44
0:07:44
 0:10:37
0:10:37
 0:59:59
0:59:59
 0:06:44
0:06:44
 0:05:56
0:05:56
 0:10:08
0:10:08
 0:09:57
0:09:57
 0:07:14
0:07:14
 0:08:20
0:08:20
 0:09:52
0:09:52
 0:04:11
0:04:11
 0:15:05
0:15:05
 0:06:41
0:06:41