filmov
tv
Solving a rational equation with two solutions
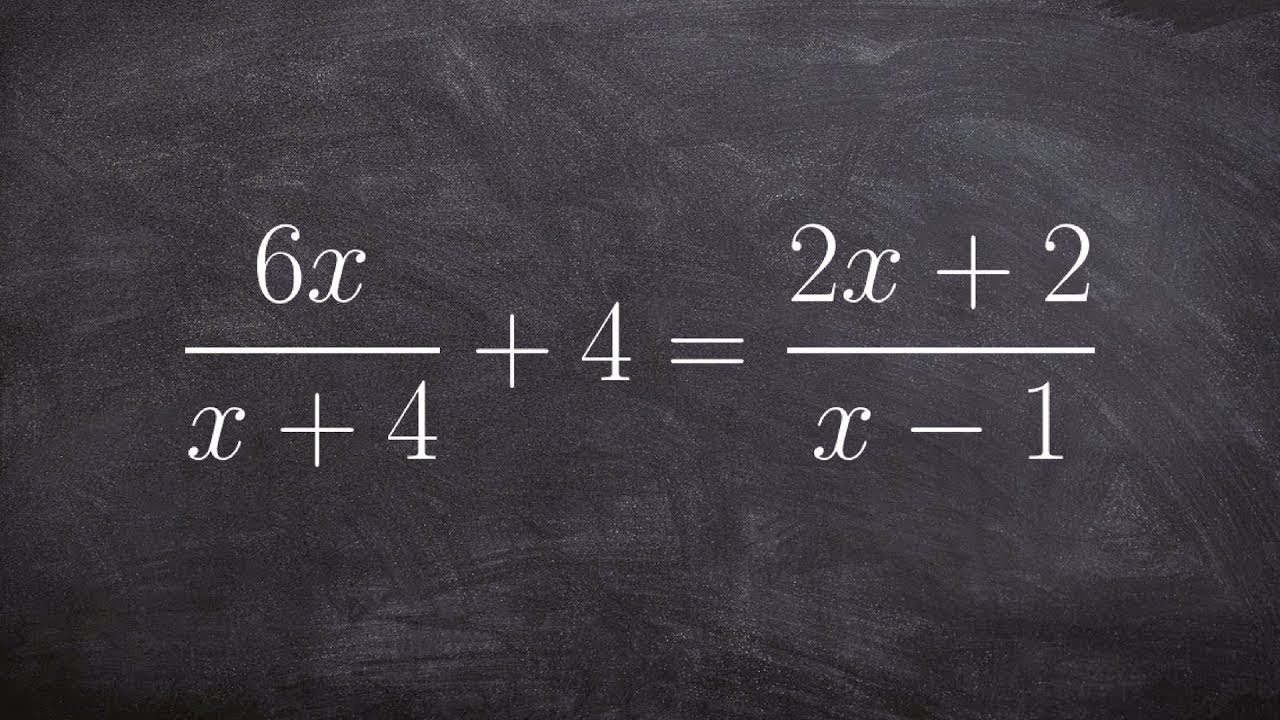
Показать описание
👉 Learn how to solve rational equations. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. There are many ways to solve rational equations, one of the ways is by multiplying all the individual rational expressions by the lowest common multiply (LCM) of the denominators. This eliminates the denominators and then we can evaluate the resulting equation accordingly.
It is very helpful to check your results by substituting them into the original equation to see if they are true. This also helps to identify the extraneous solutions. An extraneous solution is a solution that is obtained during the course of solving an equation but which does not hold true for the original equation.
Timestamps:
0:00 Intro
0:26 Start of Problem
Corrections:
5:16 It is positive 6x, not 2x.
Organized Videos:
✅ How to Solve Rational Equations
✅ How to Solve Rational Equations with Trinomials
✅ How to Solve Rational Equations with Binomials
✅ How to Solve Rational Equations with Monomials
✅ How to Solve Rational Equations with an Integer
✅ How to Solve Rational Equations | Learn About
✅ How to Solve Proportions with Binomials
✅ How to Solve Proportions with Trinomials
Connect with me:
#rationalfunctions #brianmclogan
It is very helpful to check your results by substituting them into the original equation to see if they are true. This also helps to identify the extraneous solutions. An extraneous solution is a solution that is obtained during the course of solving an equation but which does not hold true for the original equation.
Timestamps:
0:00 Intro
0:26 Start of Problem
Corrections:
5:16 It is positive 6x, not 2x.
Organized Videos:
✅ How to Solve Rational Equations
✅ How to Solve Rational Equations with Trinomials
✅ How to Solve Rational Equations with Binomials
✅ How to Solve Rational Equations with Monomials
✅ How to Solve Rational Equations with an Integer
✅ How to Solve Rational Equations | Learn About
✅ How to Solve Proportions with Binomials
✅ How to Solve Proportions with Trinomials
Connect with me:
#rationalfunctions #brianmclogan
Комментарии
 0:11:03
0:11:03
 0:04:33
0:04:33
 0:06:32
0:06:32
 0:12:06
0:12:06
 0:04:29
0:04:29
 0:12:57
0:12:57
 0:11:14
0:11:14
 0:08:50
0:08:50
 0:42:26
0:42:26
 0:03:03
0:03:03
 0:04:12
0:04:12
 0:06:17
0:06:17
 0:05:33
0:05:33
 0:06:27
0:06:27
 0:17:32
0:17:32
 0:07:20
0:07:20
 0:08:54
0:08:54
 0:02:27
0:02:27
 0:05:33
0:05:33
 0:01:23
0:01:23
 0:06:01
0:06:01
 0:04:08
0:04:08
 0:05:31
0:05:31
 0:04:46
0:04:46