filmov
tv
Comparing, which Is Larger? Learn this trick!
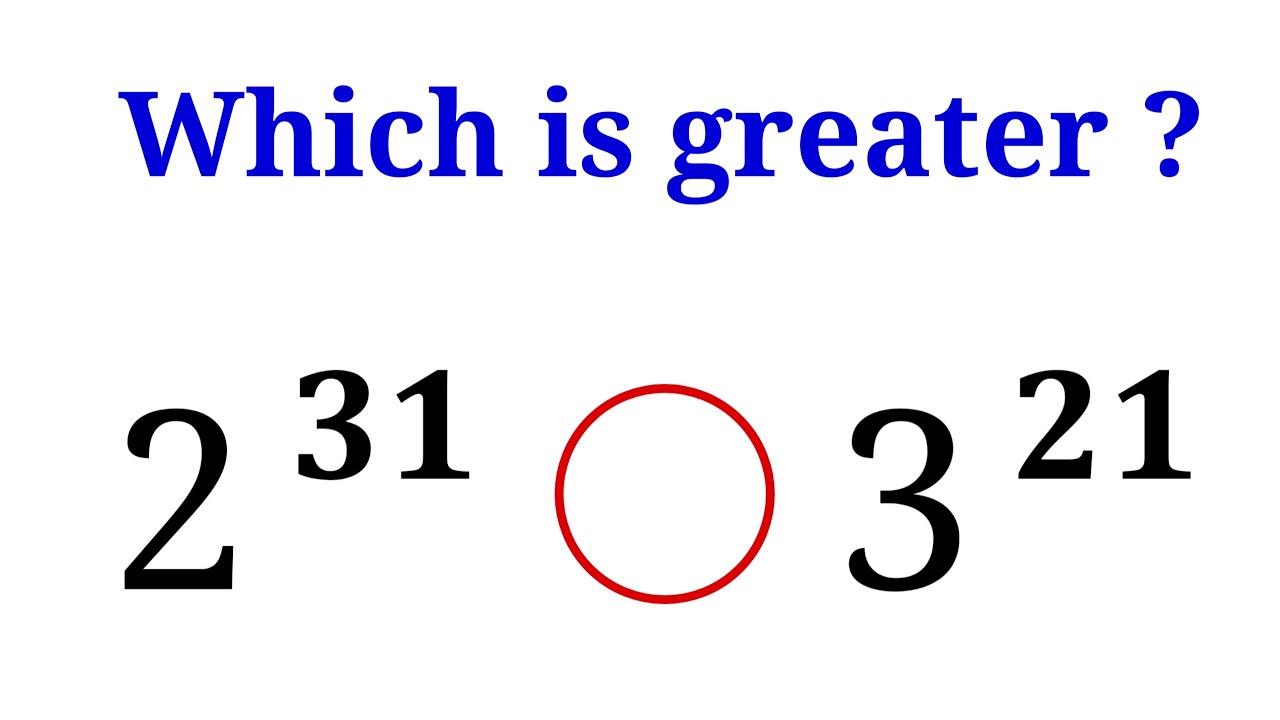
Показать описание
9^63 and 6^93, which one is larger? A fantastic math problem. A common method to this kind of questions.
Comparing, which Is Larger? Learn this trick!
Comparing Fractions 📚
Nice Comparing, Which Is Larger? | You should learn this method!!!
Comparing Fractions - Which is greater? Which is smaller? Fraction Problems | Learn about Fractions
55^44 vs 44^55 | Learn How to compare which is larger, 99% fail to solve | Math Olympiad Problem
Comparison | Which one is larger...? #mathematics #maths #shorts #learn
Which fraction is largest?🤝 #shorts #fractions #khantrickster
Big Bigger Biggest (Original Learning Time Fun Song) | COMPARE the SIZES for KIDS
More and Less | Comparison for Kids | Learn Pre-School Concepts with Siya | Part 5
Topic: Learn | Compare Large Numbers Up to 9 Digits | Conceptual Maths Grade 5 | Animated Content
Comparing Numbers | GREATER THAN | Kids Learning Videos | Comparison for Kids | Fun Learning
Longer and Shorter & Longest and Shortest | Comparison for Kids | Learn Pre-School Concepts
comparing: 5^22 and 3^33 , which is larger? you should learn this tricks #math
2 Trillion Galaxies? The Mind-Boggling Scale of the Universe Explained
Comparing Fractions #math #shorts #tutor #mathtrick #learning #fraction #bigger
Guess Who Has the Higher Grade
Comparing Numbers/Sets: Greater than, Less than, and Equal | Learning Math with Teacher Ira
Comparison.which is larger ? #maths #easymaths #easymathtricks #learning #learn #competition#algebra
Comparing numbers l Bigger and smaller number l learn to compare number for kids
World Ocean Day - June 8 #shorts
Percentage Trick Vs Reality
Team Medium Rare or Well Done? #shorts
Big and Small | Comparison for Kids | Learn Pre-School Concepts with Siya | Part 1
Large Numbers
Комментарии
 0:08:49
0:08:49
 0:00:16
0:00:16
 0:09:08
0:09:08
 0:05:13
0:05:13
 0:03:19
0:03:19
 0:00:11
0:00:11
 0:00:31
0:00:31
 0:03:25
0:03:25
 0:01:35
0:01:35
 0:03:03
0:03:03
 0:08:34
0:08:34
 0:01:52
0:01:52
 0:03:14
0:03:14
 0:01:00
0:01:00
 0:00:24
0:00:24
 0:00:29
0:00:29
 0:08:58
0:08:58
 0:01:08
0:01:08
 0:04:15
0:04:15
 0:00:10
0:00:10
 0:00:22
0:00:22
 0:00:29
0:00:29
 0:01:40
0:01:40
 0:00:58
0:00:58