filmov
tv
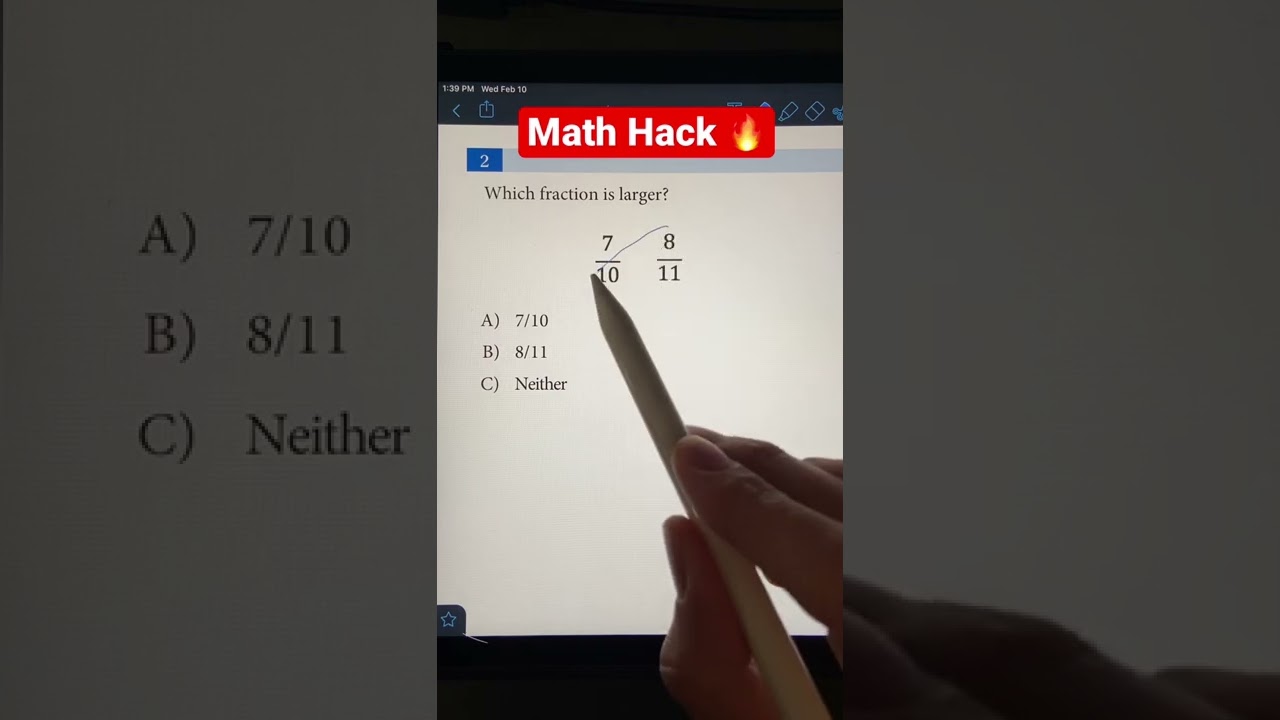
Comparing Fractions 📚
Показать описание
Math Antics - Comparing Fractions
Comparing Fractions | How to Compare Fractions
Comparing Fractions for Kids | Easy Math Lessons
Comparing Fractions With Different Denominators
Comparing Fractions Song | Less Than Greater Than | Ordering Fractions From Least to Greatest
Comparing Fractions
Comparing and Ordering Fractions with Different Denominators (fraction strips)
Comparing fractions visually - easy lesson for 2nd grade
Mastering Operations on Fractions | Addition, Subtraction, Multiplication, and Division Simplified |
Comparing Fractions - 4th Grade Mage Math
Compare Fractions with the Same Denominator. Grade 3
Comparing Fractions 📚
Comparing Fractions | MathHelp.com
Comparing fractions | Fractions | Pre-Algebra | Khan Academy
Comparing Fractions - compare fractions instantly!
How to determine which Fraction is larger
Comparing Fractions - 3rd Grade Mathematics Video for Kids
Comparing Fractions With Different Denominators | The Maths Guy
Comparing Fractions Using Common Denominators - [4-6-7]
3rd Grade Comparing Fractions Strategies
Compare Fractions with the Same Numerator. Grade 3
Comparing & Ordering Fractions for Beginners
What are Benchmark Fractions? | Comparing & Ordering #steamspiration
Comparing Unit Fractions
Комментарии
 0:06:31
0:06:31
 0:07:43
0:07:43
 0:06:05
0:06:05
 0:10:12
0:10:12
 0:03:52
0:03:52
 0:06:13
0:06:13
 0:04:02
0:04:02
 0:07:14
0:07:14
 0:25:20
0:25:20
 0:05:55
0:05:55
 0:01:37
0:01:37
 0:00:16
0:00:16
 0:01:21
0:01:21
 0:02:30
0:02:30
 0:03:15
0:03:15
 0:05:44
0:05:44
 0:05:40
0:05:40
 0:09:32
0:09:32
 0:24:21
0:24:21
 0:04:55
0:04:55
 0:01:50
0:01:50
 0:03:38
0:03:38
 0:02:56
0:02:56
 0:03:19
0:03:19