filmov
tv
Differential Equations, Lecture 6.6: Boundary value problems

Показать описание
Differential Equations, Lecture 6.6: Boundary value problems.
An initial value problem (IVP) is an ODE involving a function y(t) of time, with initial conditions. A boundary value problem (BVP) is an ODE involving a function y(x) of position, with boundary conditions. An example might be where y(x) measures the temperature of a rod, and the temperature at the endpoints is fixed. The theory of IVPs (existence and uniqueness of solutions) is well-understood, whereas BVPs are more mysterious. We give an 3 examples of an ODE with slightly different boundary conditions, yielding infinitely many, one, and no solutions, respectively. We conclude by solving a few variants of a classic BVP that will be very useful in our study of PDEs. In doing so, we revisit the hyperbolic trig functions: cosh and sinh.
An initial value problem (IVP) is an ODE involving a function y(t) of time, with initial conditions. A boundary value problem (BVP) is an ODE involving a function y(x) of position, with boundary conditions. An example might be where y(x) measures the temperature of a rod, and the temperature at the endpoints is fixed. The theory of IVPs (existence and uniqueness of solutions) is well-understood, whereas BVPs are more mysterious. We give an 3 examples of an ODE with slightly different boundary conditions, yielding infinitely many, one, and no solutions, respectively. We conclude by solving a few variants of a classic BVP that will be very useful in our study of PDEs. In doing so, we revisit the hyperbolic trig functions: cosh and sinh.
Separation of Variables I: Dirichlet Boundaries - Partial Differential Equations | Lecture 6
Differential Equations, Lecture 6.6: Boundary value problems
Numerical Partial Differential Equation Lecture 6 l Matlab Code For Heat Equation l ut=auxx
Partial Differential Equation Lecture 6: Method of Separation Variable example
Differential Equations: Lecture 2.5 Solutions by Substitutions
Boundary Value Problem (Boundary value problems for differential equations)
Lecture 6- Ordinary Differential Equations|| CSIR-NET/GATE || By- Eshita Ma'am
[HT-6] Boundary and Initial Conditions - Heat Diffusion Equation
MA 201: Differential Equations. Lecture 6.
Ex.4.2.Q.6.differential Equation by D.G.Zill
partial differential equation : initial value problem and boundary value problem lecture 6
Lecture 6 : Second and Higher Order Linear Ordinary Differential Equations
Differential Equations || Lec 40 || Ex: 4.4: Q6 || Undetermined Coefficients Method
Differential equations 6
Mixing Problem Differential Equation (Application)
Differential equations, a tourist's guide | DE1
6. Boundary conditions for One dimensional wave equation.
Jeff Bezos Quit Being A Physicist
Differential Equations || Lec 65 || Ex: 5.1: Q 6-9 || Free Undamped Motion, Spring Mass System
👀 Asking GCSE Students (Hamdi) How Much They Physics They Know - Part 1 #Shorts
Lecture # 25 || How to solve Boundary Value Problem || BVP || ODE
Solving Initial Value Problems, Second Order Differential Equations y''+4y'+35=36x+18
Class 12th – First Order First Degree Differential Equation Problem Example-6 | Tutorials Point
Undetermined Coefficients: Solving non-homogeneous ODEs
Комментарии
 0:34:22
0:34:22
 0:39:56
0:39:56
 0:12:23
0:12:23
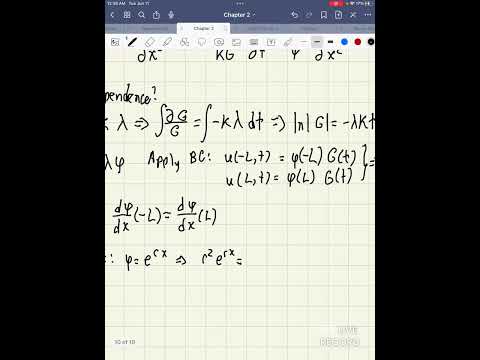 0:38:38
0:38:38
 1:42:38
1:42:38
 0:05:02
0:05:02
 0:59:15
0:59:15
![[HT-6] Boundary and](https://i.ytimg.com/vi/xpFl-Jk3Gfk/hqdefault.jpg) 0:13:51
0:13:51
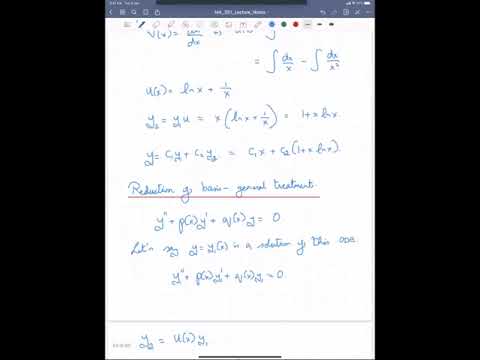 0:54:39
0:54:39
 0:03:03
0:03:03
 0:15:17
0:15:17
 0:47:20
0:47:20
 0:22:11
0:22:11
 0:17:20
0:17:20
 0:09:31
0:09:31
 0:27:16
0:27:16
 0:10:53
0:10:53
 0:00:56
0:00:56
 0:27:08
0:27:08
 0:00:37
0:00:37
 0:26:28
0:26:28
 0:13:16
0:13:16
 0:03:52
0:03:52
 0:12:44
0:12:44