filmov
tv
Separation of Variables I: Dirichlet Boundaries - Partial Differential Equations | Lecture 6
Показать описание
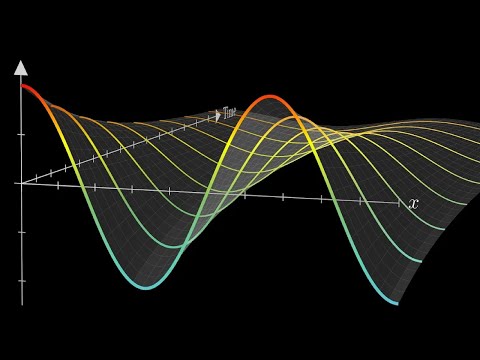
We are finally in a position to solve the heat equation! In this lecture we solve the heat equation with Dirichlet, or fixed, boundary conditions. We introduce the method of separation of variables and show that it results in an infinite series solutions whose coefficients are determined by the initial condition. Identifying these coefficients leads to a discussion of the orthogonality of sine modes, which in turn presents the Fourier sine series. Different initial conditions are illustrated, as well as a description of the long-time behaviour.
Follow @jbramburger7 on Twitter for updates.
Follow @jbramburger7 on Twitter for updates.
0:34:22
Separation of Variables I: Dirichlet Boundaries - Partial Differential Equations | Lecture 6
0:39:45
Partial Differential Equation with Dirichlet Boundary Conditions (With Example)
0:49:54
PDE 101: Separation of Variables! ...or how I learned to stop worrying and solve Laplace's equa...
0:21:17
PDE: Heat Equation - Separation of Variables
0:35:02
Oxford Calculus: How to Solve the Heat Equation
0:14:13
Solving the heat equation | DE3
0:12:53
The Dirichlet Problem For the Laplacian on a Rectangle by Separation of Variables
0:18:51
Heat Equation PDE Neumann boundary condition
0:43:11
Lecture 23 (Solving the Heat Equation with Dirichlet and Neumann conditions)
0:27:01
02. Solving the Wave Equation with Dirichlet Boundary Conditions
0:11:09
Solving the 1-D Heat/Diffusion PDE by Separation of Variables (Part 1/2)
0:28:39
07. Solving the Heat Equation with Dirichlet Boundary Conditions
0:28:50
mod07lec67 - The Laplace Equation: Dirichlet and Neumann boundary conditions
0:41:37
12.4: Wave Equation
0:18:02
Partial Differential Equations - 5.9 - Laplace's Equation - Part 1 of 2
0:32:45
12.3: Heat Equation
0:18:07
Laplace's Equation on a Rectangle
0:13:17
Laplace Equation
0:18:40
Solution of 2D Laplace Equation using Separation of Variables Method
0:37:31
Lecture 4.11: IBVP for Wave Equation - Separation of Variables Method
0:04:12
Solving the heat equation using separation of variables - example one
0:31:13
Potential Equation Solution
0:09:24
Partial Differential Equations - II. Separation of Variables
0:52:50
Introduction to Heat equation and separation of variables
Комментарии