filmov
tv
Solving & checking logarithmic equations (4 examples)
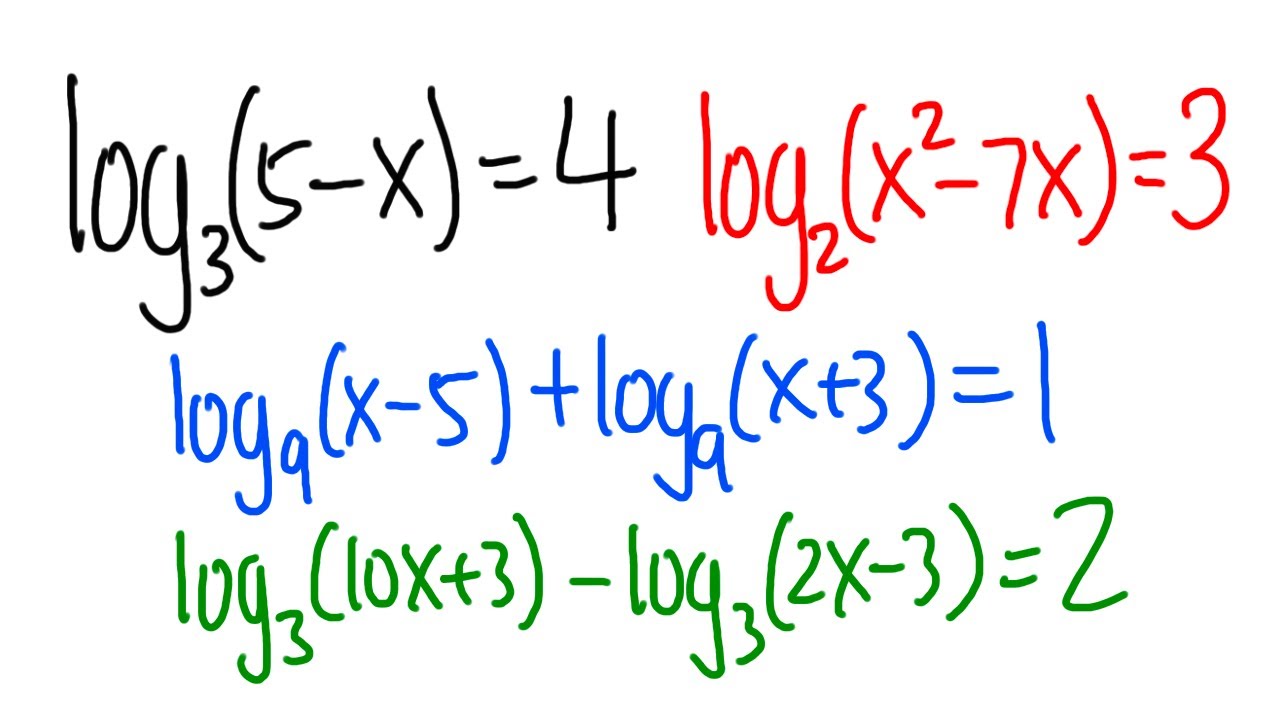
Показать описание
0:00 Q1 log_3(5-x)=4
1:39 Q2 log_2(x^2-7x)=3
3:54 Q3 log_9(x-5)+log_9(x+3)=1
6:14 Q4 log_3(10x+3)-log_3(2x-3)=2
---------------------------------------------------------
If you find this channel helpful and want to support it, then you can
join the channel membership and have your name in the video descriptions:
buy a math shirt or a hoodie:
---------------------------------------------------------
Best wishes to you,
#justcalculus #precalculus
Solving Logarithmic Equations
Solving Exponential and Logarithmic Equations
Logarithmic Equation With Extraneous Solution
SOLVING LOGARITHMIC EQUATIONS || FINDING THE VALUE OF X
Solving Logarithmic Equations | Logarithm | Laws of Logarithm | General Mathematics
Solving Logarithmic Equations... How? (NancyPi)
Solving a logarithm equation (with an extraneous solution)
Solving logarithmic equations by factoring
Olympiad Prep Logarithmic Equation | Laws of Logarithm| Factoring| Quadratic Equation
Solve Any Logarithmic Equation | Check for Extraneous Solutions | Eat Pi
Solving a simple logarithm
Solve and Check Log Equation Q7
Ex: Solve Logarithmic Equations Containing Only Logarithms
Solving Logarithmic Equations (5 Examples)
Solving Complex Logarithmic Equations
Solving logarithmic equations with extraneous solution
Restrictions when Solving Logarithmic Equation
solving a logarithmic equation with different bases
Solving A Quick and Easy Logarithmic Equation
Solving Logarithmic Equations - Example 1
Techniques for Solving Logarithmic Equations
04 - Solving Logarithmic Equations - Part 1 - Equations with Log(x)
Solving a logarithmic equation for x using factoring
Solving Exponential and Logarithmic Equations (Multiple Examples)
Комментарии
 0:25:27
0:25:27
 0:07:08
0:07:08
 0:05:11
0:05:11
 0:14:27
0:14:27
 0:13:29
0:13:29
 0:15:05
0:15:05
 0:04:07
0:04:07
 0:07:00
0:07:00
 0:25:06
0:25:06
 0:15:08
0:15:08
 0:03:03
0:03:03
 0:04:46
0:04:46
 0:05:18
0:05:18
 0:11:04
0:11:04
 0:10:42
0:10:42
 0:06:50
0:06:50
 0:07:29
0:07:29
 0:06:02
0:06:02
 0:09:26
0:09:26
 0:03:08
0:03:08
 0:09:22
0:09:22
 0:27:26
0:27:26
 0:06:10
0:06:10
 0:12:27
0:12:27