filmov
tv
Complex number solutions to polynomial equations
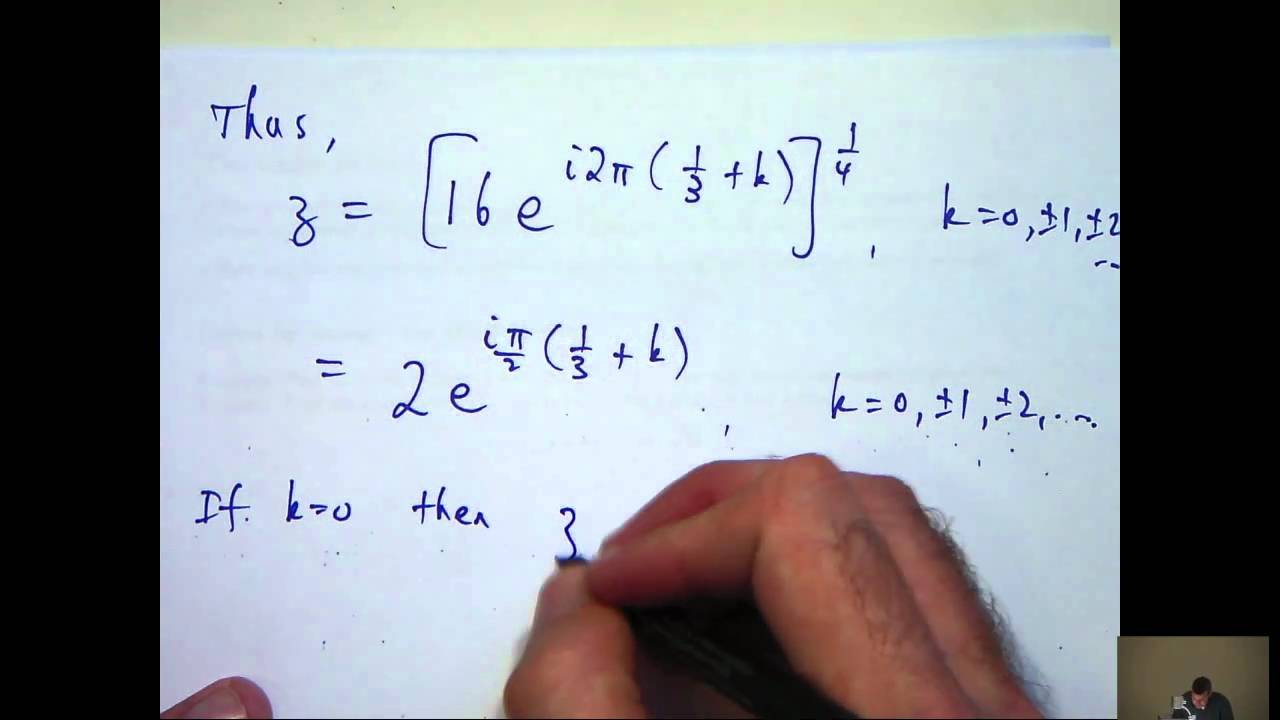
Показать описание
This video shows how to find the roots of polynomial equations. The roots are complex numbers. In this video we are going to learn how to solve polynomial equations that
involve complex numbers. Now at school you would have solved equations like quadratic
equations but when complex numbers are involved firstly you need to recognise that equations
involving complex numbers can require more care to solve. In the analysis of applied
problems we often need to solve equations and the solutions hopefully are the desired
information that we seek. Knowing how to solve polynomial equations with complex numbers
just adds to our repertoire. . 00:00-01:00.
Let us build our intuition though. How do we actually solve these types of equations? Here were
asked to find all of the complex 4th roots of this complex number here and you may leave your
answer in polar form. So let us just write out the actual equation that we are endeavouring to
solve here. And of course we want to solve this for z. Now the fundamental theorem of algebra
tells us that because of this power 4 we would expect 4 solutions to this equation. So it is our
task to go through and extract those four solutions. So how I do that? Well I am actually going to
write the right hand side here in so called polar form. So, now polar form of a complex number
involves the length r to the origin and an angle θ where θ is the angle to the positive real axis.
So what we would like to do is to calculate a specific r and a θ for this right hand side. Okay well
we can easily do that. Now the 8 here does not change anything. Usually to find the r you
usually square the coefficient, I guess each component here, and add them together and take
the square root. Now the 8 is not going to you can expand these but I am just going to leave the
8 out there for simplicity. Okay so simplify here and we will get 16. The next thing we would like
to calculate is the θ associated with this right hand side this complex number here. Well θ is just
tan inverse √(3)-1 okay so again the 8 is not going to change anything here. Now this complex
number here is going to lie in this second quadrant. Now what I can do is draw a little right angle
triangle and then use basic trigonometry. So if this angle here is α what I am interested here is
this θ here. Okay so simple trig using this tan inverse will give me α = π/3. So θ then will give
me (2*π)/3 so combining this and this we can now solve the following. Now how does this help
us? Well we can take the 4th roots of the both sides and then simplify. Now this is where it gets
a little bit tricky. You can just use your index laws here and if you wanted to you could expand
this but there is a danger there. If I expanded this I would get one value for z. But again by the
fundamental theorem of algebra we would expect there to be 4 solutions here where as if I just
expanded this I would only get one solution. So what can I do? Well a good idea is to use the
fact that this complex number can be produced by going out and spinning around 2*π radians
around the origin. So I can actually write it like this. Plus i*2*π*k. Now where k=0, +/- 1, +/-2 etc
okay now what I am going to do now is simplify this and then expand as I normally would. Okay
so I should have something like this and then let us bring that quarter in and simplify. Okay so
now we are in a position where you can just substitute various simple values for k and we will
get different roots for our polynomial. If k=0 then I am going
to get, I am just going to put a subscript here to note that this is associated with the k=0 value
so this disappears and I get (i*π)/6. let us choose another one k=1 I go up here I add these
together I get 4/3 and then simplify and I should get something like this. Okay that is another
one. So let us keep on going let us do k=-1 now, I guess this should be lower case, so I go up
here I substitute k=-1 and then I simplify. If I do that then I will get the following and finally well I
could put in positive 2 there but I am actually going to put in negative 2 and you will see why in a
minute. Okay now the important thing is these coefficient of i should be strictly greater than -π
but less than or equal to π. Okay if I put in k=+2 here then I wouldn't get that simplification. So I
have got 4 roots here I have solved the equation they are all in polar form and what I am going
to do now is plot these complex numbers on a diagram. we are not asked to do that but I think it
is important anyway. So I am going out 2 units. Okay and I am going to plot my various
solutions so I go out 2 units and rotate anticlockwise π/6 radians so that would be z0. Then I go
out 2 units and rotate 2*π/3 radians so this would be z_1. Again I rotate π/3 in the clockwise
direction to get z-1 and keep on going to get z-2. Okay so let us look at the bigger picture.
01:00- 10:06.
involve complex numbers. Now at school you would have solved equations like quadratic
equations but when complex numbers are involved firstly you need to recognise that equations
involving complex numbers can require more care to solve. In the analysis of applied
problems we often need to solve equations and the solutions hopefully are the desired
information that we seek. Knowing how to solve polynomial equations with complex numbers
just adds to our repertoire. . 00:00-01:00.
Let us build our intuition though. How do we actually solve these types of equations? Here were
asked to find all of the complex 4th roots of this complex number here and you may leave your
answer in polar form. So let us just write out the actual equation that we are endeavouring to
solve here. And of course we want to solve this for z. Now the fundamental theorem of algebra
tells us that because of this power 4 we would expect 4 solutions to this equation. So it is our
task to go through and extract those four solutions. So how I do that? Well I am actually going to
write the right hand side here in so called polar form. So, now polar form of a complex number
involves the length r to the origin and an angle θ where θ is the angle to the positive real axis.
So what we would like to do is to calculate a specific r and a θ for this right hand side. Okay well
we can easily do that. Now the 8 here does not change anything. Usually to find the r you
usually square the coefficient, I guess each component here, and add them together and take
the square root. Now the 8 is not going to you can expand these but I am just going to leave the
8 out there for simplicity. Okay so simplify here and we will get 16. The next thing we would like
to calculate is the θ associated with this right hand side this complex number here. Well θ is just
tan inverse √(3)-1 okay so again the 8 is not going to change anything here. Now this complex
number here is going to lie in this second quadrant. Now what I can do is draw a little right angle
triangle and then use basic trigonometry. So if this angle here is α what I am interested here is
this θ here. Okay so simple trig using this tan inverse will give me α = π/3. So θ then will give
me (2*π)/3 so combining this and this we can now solve the following. Now how does this help
us? Well we can take the 4th roots of the both sides and then simplify. Now this is where it gets
a little bit tricky. You can just use your index laws here and if you wanted to you could expand
this but there is a danger there. If I expanded this I would get one value for z. But again by the
fundamental theorem of algebra we would expect there to be 4 solutions here where as if I just
expanded this I would only get one solution. So what can I do? Well a good idea is to use the
fact that this complex number can be produced by going out and spinning around 2*π radians
around the origin. So I can actually write it like this. Plus i*2*π*k. Now where k=0, +/- 1, +/-2 etc
okay now what I am going to do now is simplify this and then expand as I normally would. Okay
so I should have something like this and then let us bring that quarter in and simplify. Okay so
now we are in a position where you can just substitute various simple values for k and we will
get different roots for our polynomial. If k=0 then I am going
to get, I am just going to put a subscript here to note that this is associated with the k=0 value
so this disappears and I get (i*π)/6. let us choose another one k=1 I go up here I add these
together I get 4/3 and then simplify and I should get something like this. Okay that is another
one. So let us keep on going let us do k=-1 now, I guess this should be lower case, so I go up
here I substitute k=-1 and then I simplify. If I do that then I will get the following and finally well I
could put in positive 2 there but I am actually going to put in negative 2 and you will see why in a
minute. Okay now the important thing is these coefficient of i should be strictly greater than -π
but less than or equal to π. Okay if I put in k=+2 here then I wouldn't get that simplification. So I
have got 4 roots here I have solved the equation they are all in polar form and what I am going
to do now is plot these complex numbers on a diagram. we are not asked to do that but I think it
is important anyway. So I am going out 2 units. Okay and I am going to plot my various
solutions so I go out 2 units and rotate anticlockwise π/6 radians so that would be z0. Then I go
out 2 units and rotate 2*π/3 radians so this would be z_1. Again I rotate π/3 in the clockwise
direction to get z-1 and keep on going to get z-2. Okay so let us look at the bigger picture.
01:00- 10:06.
0:03:10
Factoring polynomials using complex numbers | Khan Academy
0:11:07
Complex number solutions to polynomial equations
0:12:52
How To Find The Real & Imaginary Solutions of Polynomial Equations
0:17:32
Introduction to Complex Solutions of Polynomials (Precalculus - College algebra 35)
0:08:41
Complex Roots of Polynomials
0:11:07
How to solve polynomial equations involving complex numbers. Chris Tisdell UNSW Sydney
0:05:35
Finding All of the Zeros of a Polynomial Including Complex
0:27:11
15D - Complex Solutions to Polynomial Equations
0:05:28
Solving using the quadratic formula with complex solutions
0:05:54
Find Complex Roots of a Cubic Equation z^3 - 3z^2 + z + 5 = 0
0:02:07
Solving Equations With Complex Numbers
0:17:39
Alg2 7.2 Finding Complex Solutions of Polynomial Equations
0:00:50
5 simple unsolvable equations
0:05:06
Determine the number of positive, negative and complex roots of a polynomial
0:04:51
Given complex zeros find the polynomial - Online Tutor
0:23:28
Polynomial Equations with Complex Solutions IB Math Pre University Calculus
0:09:28
Complex Numbers : Roots of a quadratic equation - conjugate pairs : ExamSolutions
0:40:23
Creating Polynomials from Complex Solutions (Precalculus - College Algebra 36)
0:03:11
Roots of a polynomial equation. Finding the real and complex zeros of a polynomial
0:05:47
Imaginary Numbers Are Real [Part 1: Introduction]
0:09:01
Precalculus 12.1a - Complex Quadratic
0:10:15
Example: Complex roots for a quadratic | Algebra II | Khan Academy
0:02:43
How to find the roots of a polynomials by factoring
0:04:08
Learn How to Find the Real and Complex Zeros from Factoring
Комментарии