filmov
tv
Prove Square Roots of Non-Perfect Squares are Irrational

Показать описание
Real Analysis Proofs, Video #1. Use the Fundamental Theorem of Arithmetic (Unique Prime Factorization).
(0:00) Real Analysis Proofs, Video #1
(0:53) Notation and problem statement
(1:19) We are assuming the square root of n exists
(2:10) This is a proof by contradiction
(3:15) Then x=a/b, where, WLOG, a and b are relatively prime (gcd(a,b)=1)
(5:38) Square and use the Fundamental Theorem of Arithmetic
(8:24) Use the fact that n is not a perfect square
(9:57) Use nb^2=a^2 to say pj divides a
(12:07) pj divides b
(13:45) This is a contradiction
(14:36) The original assumption must be wrong and x is not rational
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Proof that the square root of ANY integer is irrational (besides perfect squares)
Prove Square Roots of Non-Perfect Squares are Irrational
How to Simplify the Square Root of a Non Square Number
Find Square Root by Hand without Calculator
A Proof That The Square Root of Two Is Irrational
why sqrt(36) is just positive 6
Proof that square root of prime number is irrational | Algebra I | Khan Academy
Proof: Square Root of 2 is Irrational
CBSE Maths 8 RS Aggarwal | Cubes and Cube Roots | Part 1
overpowered irrationality! #math #proof #squareroot
How to Approximate Square Root of a Number
Proof: Square Root of 3 is Irrational
World's Fastest Square Root: Newton's Method
Murdered Over a Math Proof?! Irrational Numbers and the Square Root of 2
If a number is not a perfect square, then its square root is irrational | Real numbers | Concepts
To Prove That Root-N is an Irrational Number
Square root of ANY number instantly - shortcut math.
A superior proof of the irrationality of square roots.
Prove Square Root of 6 is Irrational
Prove that sqrt(2) + sqrt(3) Cannot be a Rational Number
How Square Roots Can Help You Check Prime Numbers
Finding square root of non perfect square numbers | Estimation Method | One decimal place :- 2
How to Estimate the Square Root of Non-Square Numbers #22
Prove that √𝑛 is not a rational number, if n is not a perfect square.
Комментарии
 0:06:00
0:06:00
 0:15:27
0:15:27
 0:02:52
0:02:52
 0:09:30
0:09:30
 0:17:22
0:17:22
 0:01:42
0:01:42
 0:07:28
0:07:28
 0:04:02
0:04:02
 1:21:58
1:21:58
 0:00:44
0:00:44
 0:00:52
0:00:52
 0:06:13
0:06:13
 0:02:18
0:02:18
 0:10:09
0:10:09
 0:07:53
0:07:53
 0:04:16
0:04:16
 0:08:02
0:08:02
 0:12:53
0:12:53
 0:04:19
0:04:19
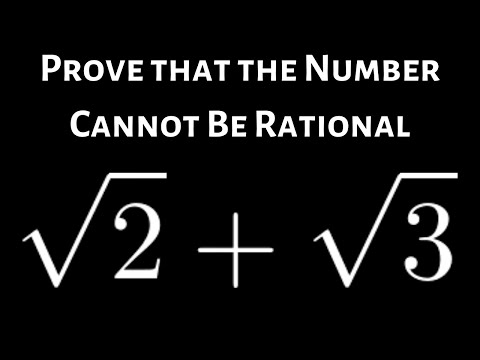 0:05:34
0:05:34
 0:09:16
0:09:16
 0:05:21
0:05:21
 0:02:21
0:02:21
 0:04:24
0:04:24