filmov
tv
Square root of ANY number instantly - shortcut math.
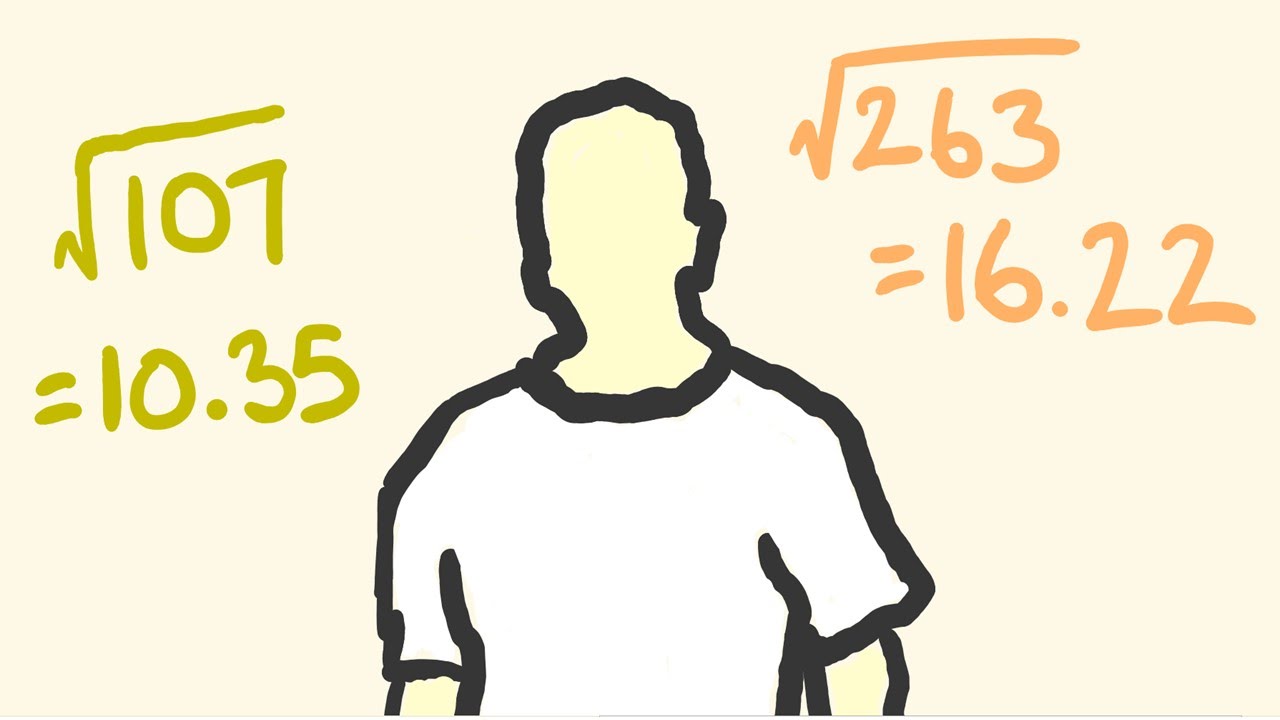
Показать описание
This math trick allows you to work out the square root of any number - NOT JUST PERFECT SQUARES - instantly. With decimals. With ease. Can you work faster than a calculator? With this tecmath trick you just might! The math shortcut magic is back!
Square root of ANY number instantly - shortcut math.
Square root in 3 seconds - math trick
How To Find The Square Root of Large Numbers Mentally
Find Square Root by Hand without Calculator
What are Square Roots? | Math with Mr. J
Take Any Square Root by Hand - Easy to Learn!
How To Calculate Square Roots - Numerals That Changed Math Forever
How to Calculate Square Root Without Calculator
Square root of addition of consecutive number cube🔥|| Math tricks #shorts #viral #trending #ytshorts...
Calculating Square Root by Hand (Early Grades)
Square Root of a Number using Long Division Method - Part 1 | Exponents | Infinity Learn
Imperfect Square Root in 5 Sec | Number from 1 to 9999 | Trick for JEE & NEET | Mohit Sir [IIT K...
Square root trick! Long division method
Finding Square Root Using Long Division|Perfect Square #longdivisionmethod #squareroot
How to find square root of any number
Math Antics - Exponents and Square Roots
How to calculate faster than a Calculator- Square Root Mental Maths - 9
Finding Square Root Using Long Division | Perfect Square #longdivisionmethod #squareroot
Quickest Way to find Square Root of two Numbers | Vedic Maths tricks for fast calculation
Square Root in 4 Seconds 🔥 | Special Method | SBI / IBPS / RRB / SSC / CAT | Aashish Arora
Square Roots Long Division method
How to Simplify the Square Root of a Non Square Number
Square Root By Long Division Method | Squares and square roots class 8th | Division Method
SQUARE ROOT TRICK | SQUARE ROOT OF ANY NUMBER | IN 5 SECONDS | CAREER DEFINER | KAUSHIK MOHANTY
Комментарии
 0:08:02
0:08:02
 0:09:46
0:09:46
 0:12:37
0:12:37
 0:09:30
0:09:30
 0:04:00
0:04:00
 0:10:12
0:10:12
 0:10:16
0:10:16
 0:05:48
0:05:48
 0:00:17
0:00:17
 0:07:24
0:07:24
 0:08:46
0:08:46
 0:03:19
0:03:19
 0:01:00
0:01:00
 0:00:58
0:00:58
 0:05:49
0:05:49
 0:11:09
0:11:09
 0:08:25
0:08:25
 0:01:00
0:01:00
 0:05:27
0:05:27
 0:28:45
0:28:45
 0:14:25
0:14:25
 0:02:52
0:02:52
 0:13:22
0:13:22
 0:09:22
0:09:22